以下内容皆基于鱼书《深度学习入门基于python的理论与实现》

从感知机到神经网络

感知机回顾

用图来表示神经网络，类比感知机，我们把左边的一列称为输入层，最右边的称之为输出层，中间的称为中间层(也称为隐藏层，因为神经元肉眼看不见)，我们知道当感知机接受$x_1,x_2$两个输入信号，输出$y$时，可以用如下的数学式来表示

$b$是偏置，用于控制神经元被激活的容易程度，而$w_1,w_2$是表示各个信号的权重的参数，用于控制各个信号的重要性

我们现在可以通过调用一个函数来替代(1)中分case讨论的情况来简化(1)，改写成如下形式

激活函数引入

刚才的h(x)把输入信号的总和转换成了输出信号，h(x)就被称为激活函数(activation function)

现在进一步改写式(2)，写成如下形式

首先，式(4)计算加权输入信号的和偏置的总和，然后用(5)的h函数转换为输出

激活函数

sigmoid函数

神经网络中经常使用的一个激活函数就是sigmoid函数

实际上，感知机和神经网络的主要区别就在于激活函数，其他方面基本都是一样的

阶跃函数的实现

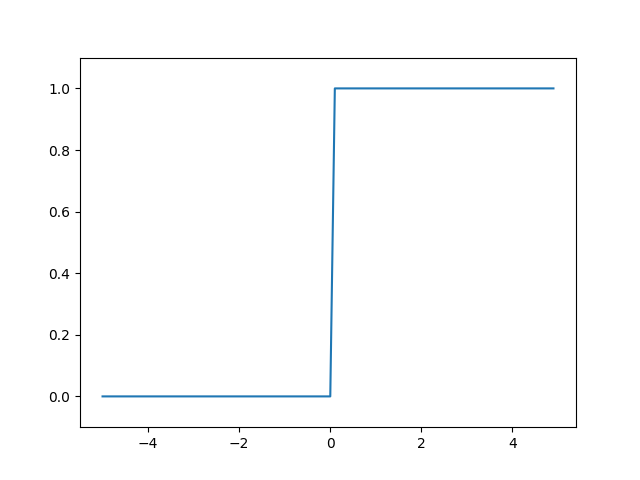
阶跃函数如(3)所示，当输入超过0时，输出1，否则输出0，可以用如下代码简单实现

1
2
3
4
5

def step_function(x):
  if x > 0:
    return 1
  else:
    return 0

这个代码中参数x只能接受实数。例如不允许step_function(np.array([1.0,2.0]))，所以我们把它修改为支持NumPy数组的实现

1
2
3

def step_function(x):
  y = x > 0
  return y.astype(np.int)

阶跃函数的图形

接下来我们就用图来表示上面定义的阶跃函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
  return np.array(x > 0,dtype=np.int)

x = np.arange(-5.0,5.0,0.1)
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1) #y轴范围
plt.show()

sigmoid函数的实现

1
2

def sigmoid(x):
  return 1 / (1 + np.exp(-x))

之所以sigmoid函数的实现支持NumPy数组，就是因为NumPy的广播功能，如果在标量和NumPy数组之间进行运算，标量会和NumPy数组的各个元素进行运算，np.exp(-x)会生成NumPy数组，所以1/(1 + np.exp(-x))的运算将会在NumPy数组的各个元素间进行

sigmoid函数和阶跃函数的比较

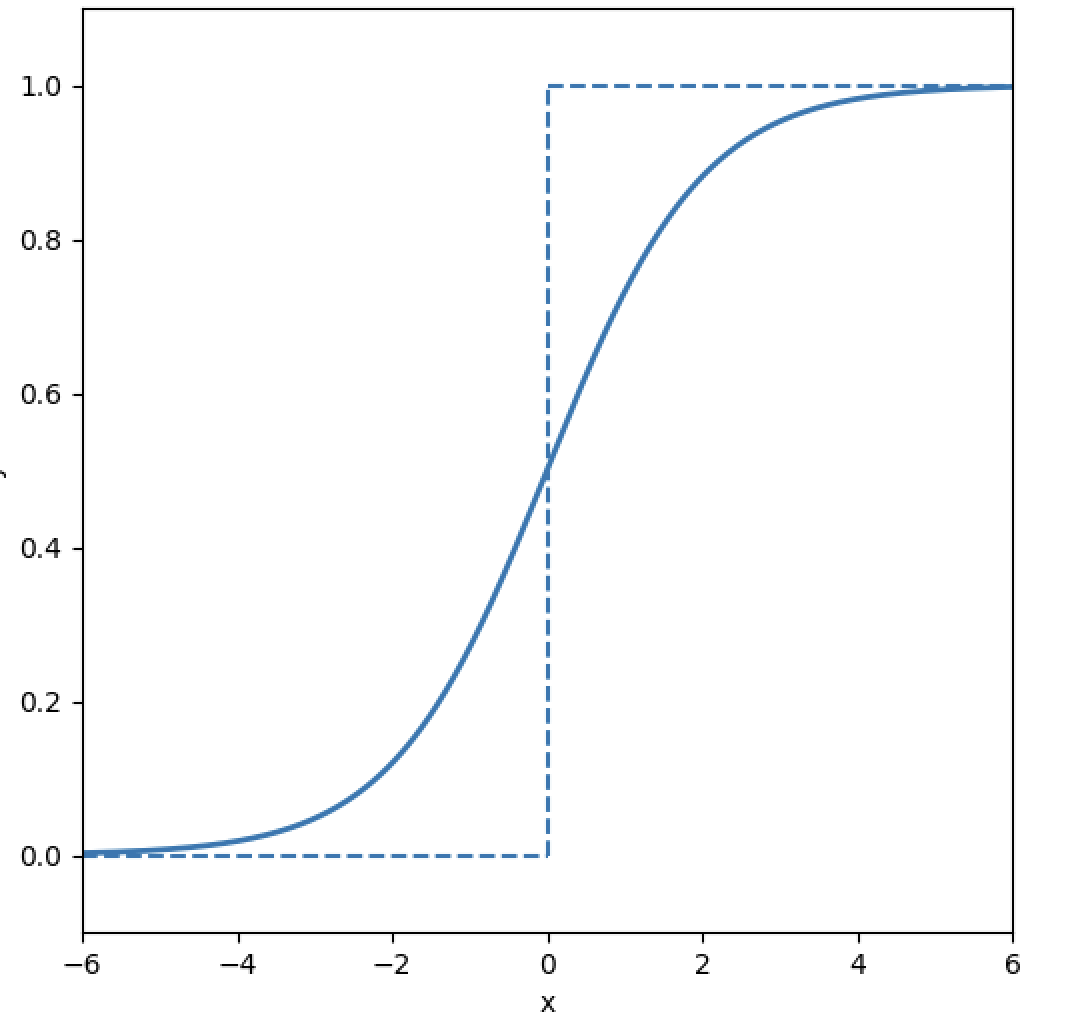
观察可以发现，首先区别就是平滑性，sigmoid函数是一条平滑的曲线，输出随着输入发生连续性的变化。而阶跃函数以0为界，输出发生急剧性的变化。因此我们可以知道，感知机的神经元之间流动的是0或1的二元信号，神经网络中流动的是连续的实数值信号。

然后说一下阶跃函数和sigmoid函数的共同性质，两者的结构均是“输入小时输出接近0；输入大时，输出靠近1”，以及不管输入是什么值，输出信号的值都在0和1中间

非线性函数

阶跃函数和sigmoid函数都是非线性函数

神经网络的激活函数必须使用非线性函数，因为如果使用线性函数，加深神经网络的层数就没有意义了（应该很好理解，很多线型函数复合仍然是线性的，就不具体说了）

ReLU函数

最近比较常见的是ReLU函数

ReLU函数在输入大于0时，直接输出该值；在输入小于等于0的时候，输出0

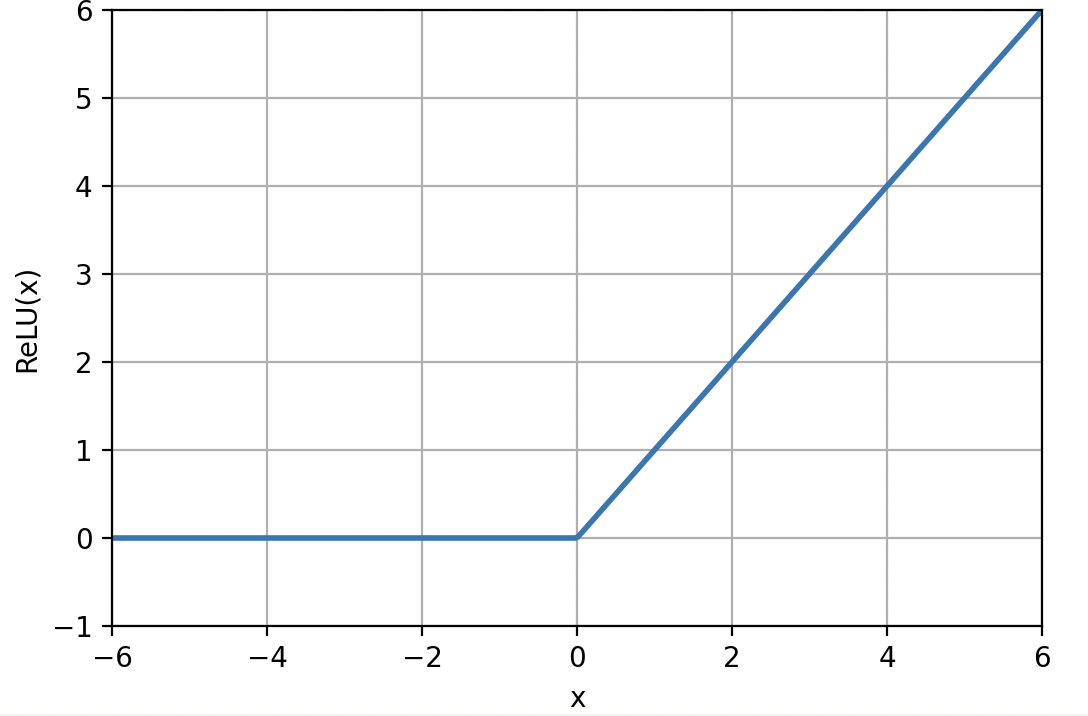
ReLU函数可以表示为以下数学式

ReLU函数的实现也非常简单

1
2

def relu(x):
  return np.maximum(0,x)

多维数组的运算

多维数组

首先假定有一个一维数组A = np.array[1,2,3,4]，数组的维数可以通过np.ndim得到。数组的形状可以通过实例变量shape获得，A由四个元素构成，是一维的，所以A.shape就是（4，），这个结果是个元组，这个一维数组为了保证和多维一样的格式，所以仍然被写成元组

矩阵乘法

不再赘述

神经网络的内积