鱼书笔记-误差反向传播法

计算图

用计算图求解

我们先来看一个简单的问题

问题：太郎在超市买了2个100日元一个的苹果，消费税是10%，请计算支付金额

如何用计算图表示，这个非常简单，小学生都能看懂

或者也可以把运算的数字放在圆圈外面，如下图

上面说的这种便是正向传播运算，也就是我们的正常运算的逻辑，但是这章的主题是反向传播，我们来看看这是什么

反向传播

加法节点的反向传播

以z=x+y为例，左图为正向传播，右图为反向传播

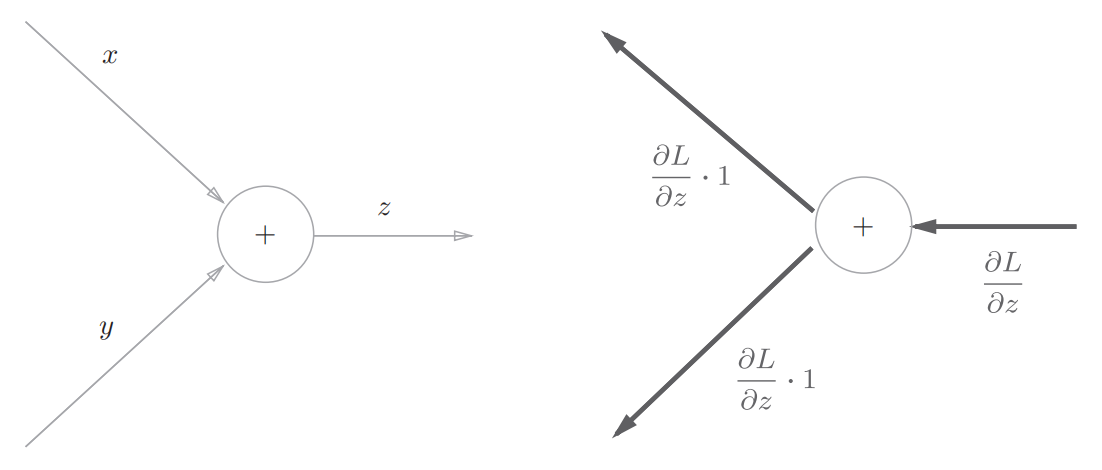
乘法节点的反向传播

以z=xy为例

回到开头的例子

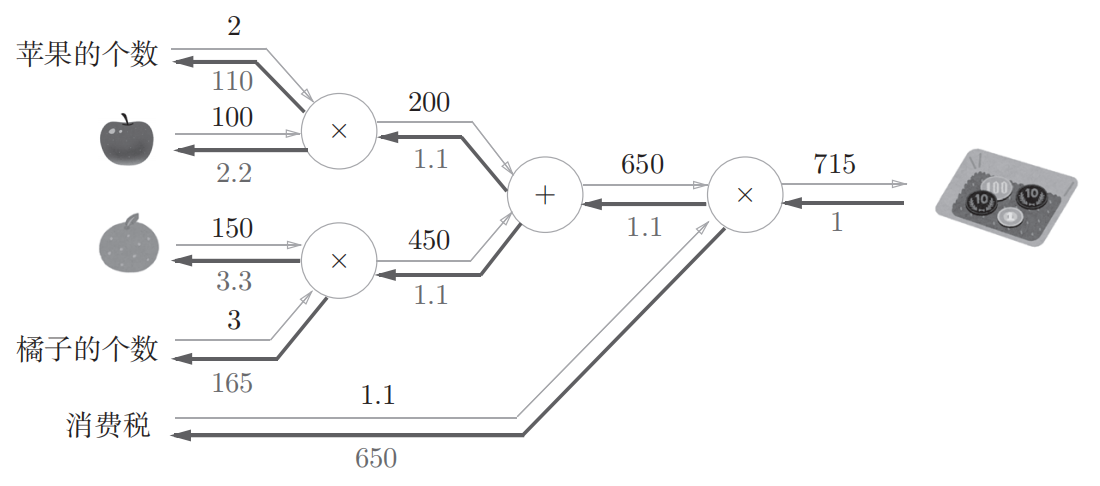
所以重新思考开头的那个买苹果的例子，要解的就是苹果的价格，苹果的个数，消费税这三个变量之间各自如何影响最终支付的金额，相当于求“支付金额关于苹果价格的导数”，“支付金额关于苹果个数的导数“，”支付金额关于消费税的导数”，反向传播的过程如下图

如图，苹果价格的导数是2.2，苹果个数的导数是110，消费税的导数是200，意思就是，如果消费税和苹果的价值增长同样的值，消费税将对最终金额产生200倍左右的影响，苹果的价格将产生2.2倍大小的影响（不过这个例子在中两者的量纲不同）

简单层的实现

本节用python实现购买苹果的例子

乘法层的实现

层的实现中有两个共通的方法forwar()和backward()。forward()对应正向传播，backward()对应反向传播。

然后来实现乘法层

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class MulLayer:
  def __init__(self):
    self.x = None
    self.y = None
   
  def forward(self,x,y):
    self.x = x
    self.y = y
    out = x * y
    
    return out
  
  def backward(self,dout):
    dx = dout * self.y
    dy = dout * self.x
    
    return dx,dy

__init__()中会初始化实例变量x和y，它们用于保存正向传播时的输出值。forward()接收x和y两个参数，将它们相乘后输出。backward()将从上游传来的导数(dout)乘以正向传播的翻转值，然后传给下游

加法层的实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class AddLayer:
  def __init__(self):
    pass
  
  def forward(self,x,y):
    out = x + y
    return out
  
  def backward(self,dout):
    dx = dout * 1
    dy = dout * 1
    return dx,dy

加法层不需要初始化，实现非常简单

例子

接下来看个实际操作的例子

上图可以像如下一样实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

#layer
mul_apple_layer = MulLayer()
mul_apple_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple,app_num)
orange_price = mul_orange_layer.forward(orange,orange_num)
all_price = add_apple_orange_layer.forward(apple_price,orange_price)
price = mul_tax_layer.forward(all,price,tax)

#backward
dprice = 1
dall_price,dtax = mul_tax_layer.backward(dprice)
dapple_price,dorange_nprice =add_apple_orange_layer.backward(dall_price)
dorange,dorange_num = mul_orange_layer.backward(dorange_price)
dapple,dapple_num = mul_apple_layer.backward(dapple_price)

print(price)
print(dapple_num,dapple,dorange_num,dtax)

激活函数层的实现

ReLU层

激活函数ReLU由下式表示

$$ y = \begin{cases} x & (x>0) \\ 0 & (x \le 0) \end{cases}\tag{1} $$

通过式(1)，可以求出y关于x的导数，如下式

$$ \frac{\partial y}{\partial x} = \begin{cases} 1 & (x>0) \\ 0 & (x \le 0) \end{cases}\tag{2} $$

接下来实现一下ReLU层

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class ReLU:
  def __init__(self):
    self.mask = None
    
  def forward(self,x):
    self.mask = (x <= 0)
    out = x.copy()
    out[self.mask] = 0
    
  def backward(self,dout):
    dout[self.mask] = 0
    dx = dout
    
    return dx

ReLU由实例变量mask。这个变量mask是由True/False构成的NumPy数组，它会把正向传播时输入的x的元素中小于等于0的地方保存为True，其他地方（大于0的元素）保存为False

Sigmoid层

接下来来实现一下sigmoid函数，sigmoid函数如下式所示

$$ y = \frac{1}{1 + \exp(-x)}\tag{3} $$

用计算图表示上式，如下所示

然后我们来看下反向传播是怎么样的

上图就是Sigmoid函数的反向传播过程，如果你看懂了上面的内容相信这个不难理解

我们在反向传输的过程中只需要专注于它的输入和输出就可以，不用在意繁琐的过程

输出的结果此外， $\frac{\partial L}{\partial y} y^{2} \exp(-x)$ 可以进一步整理如下：

$$ \begin{aligned} \frac{\partial L}{\partial y} y^{2} \exp(-x) &= \frac{\partial L}{\partial y} \frac{1}{(1+\exp(-x))^{2}} \exp(-x) \\ &= \frac{\partial L}{\partial y} \frac{1}{1+\exp(-x)} \frac{\exp(-x)}{1+\exp(-x)} \\ &= \frac{\partial L}{\partial y} \, y (1-y) \end{aligned}\tag{4} $$

实现一下Sigmoid层

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Sigmoid:
  def __init__(self):
    self.out = Nonoe
    
  def forward(self,x):
    out = 1 / (1 + np.exp(-x))
    self.out = out
    
    return out
  
  def backward(self,dout):
    dx = dout * (1.0 - self.out) * self.out
    
    return dx

Affine/Softmax层的实现

Affine层

神经网络的正向传播中，为了计算加权信号的总和，使用了矩阵的积乘运算(NumPy中是np.dot)

神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”。因此，这里将进行仿射变换的处理实现称为“Affine层”

将这里进行的求矩阵的乘积和偏置的和的运算用计算图表示出来。将乘积运算用“dot”节点表示的话，则np.dot(X,W) + B的运算可以用下图的计算图来表示出来，另外，在各个变量的上方标记了它们的形状

上图是比较简单的计算图，不过要注意X,W,B是矩阵

考虑上图的反向传播，以矩阵为对象的反向传播，按矩阵的各个元素进行计算时，步骤和以标量为对象的计算图相同。

我们可以写出计算图的反向传播，如下图

观察一下上图中各个变量的形状，X和$\frac{\partial L}{\partial \mathbf{X}}$形状相同，W和$\frac{\partial L}{\partial \mathbf{W}}$，形状相同，从下式就可以看出X和$\frac{\partial L}{\partial \mathbf{X}}$形状相同

$$ \mathbf{X} = (x_0, x_1, \cdots, x_n)\\ \frac{\partial L}{\partial \mathbf{X}} = \left( \frac{\partial L}{\partial x_0}, \frac{\partial L}{\partial x_1}, \cdots, \frac{\partial L}{\partial x_n} \right)\tag{5} $$

批版本的Affine层

前面介绍的Affine层的输入X是以单个数据为对象的。现在我们考虑N个数据一起进行正向传播的情况

下图是批版本的affine层的计算图

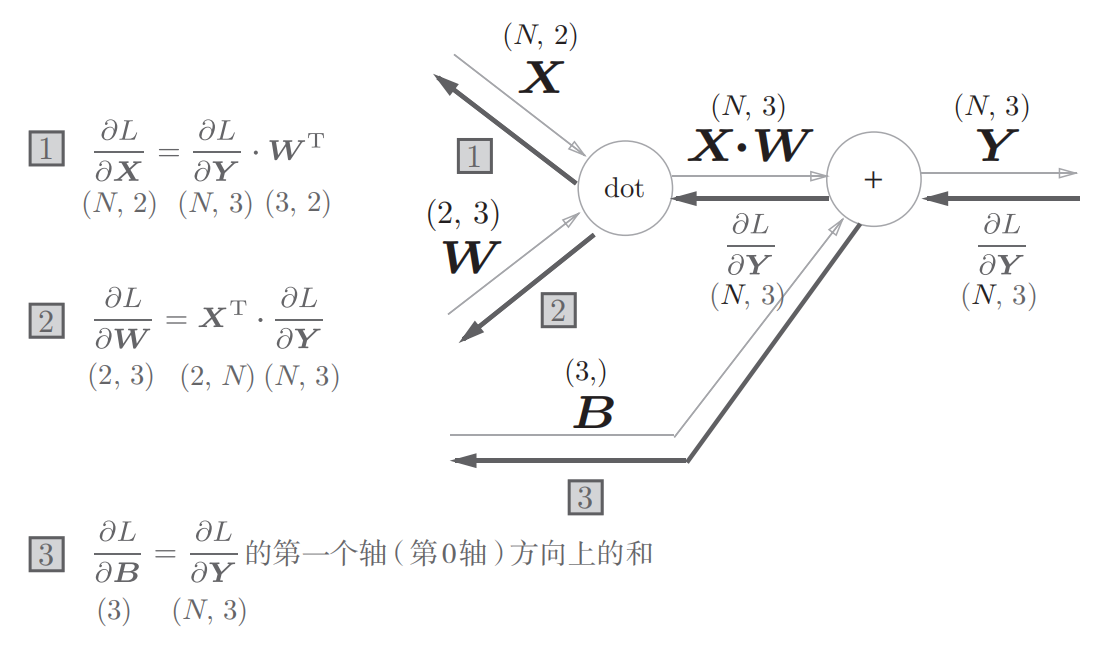
现在输入X的形状是(N,2)。之后就和前面一样

正向传播时，偏置被加到$X·W$的各个数据上。比如，N=2时，偏置会分别加到这两个数据上，因此反向传播时，各个数据的反向传播的值需要汇总为偏置的元素

Affine的实现如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Affine:
  def __init__(self,W,b):
    self.W = W
    self.b = b
    self.x = None
    self.dW = None
    delf.db = None
    
  def forward(self,x):
    self.x = x
    out = np.dot(x,self.W) + self.b
    
    return out
    
  def backward(self,dout):
    dx = np.dot(dout,self.W.T)
    self.dW = np.dot(self,x.T,dout)
    self.db = np.sum(dout,axis=0)
    
    return dx

Softmax-with-Loss层

之前说过softmax函数会将输入值正规化（将输出值的和调整为1）然后再输出。另外，因为手写数字识别要进行10类分类，所以向Softmax层的输入也有10个

下面来实现Softmax层，计算图如下图所示

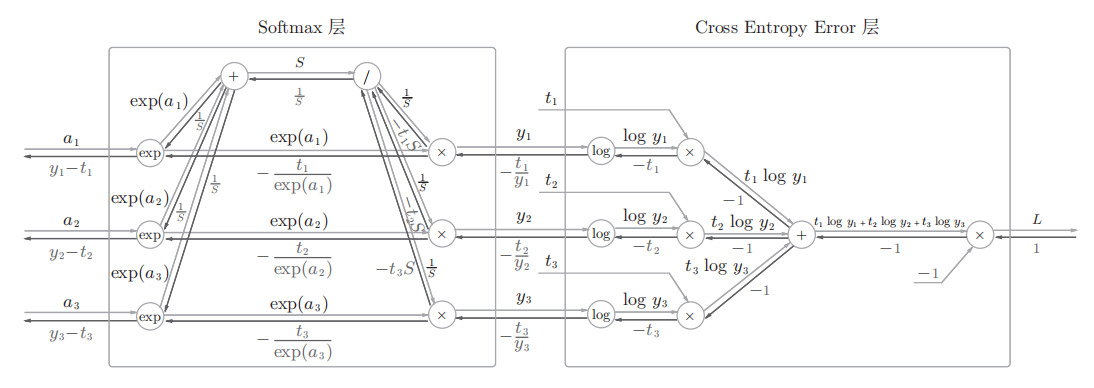
上图的计算图可以简化成下图

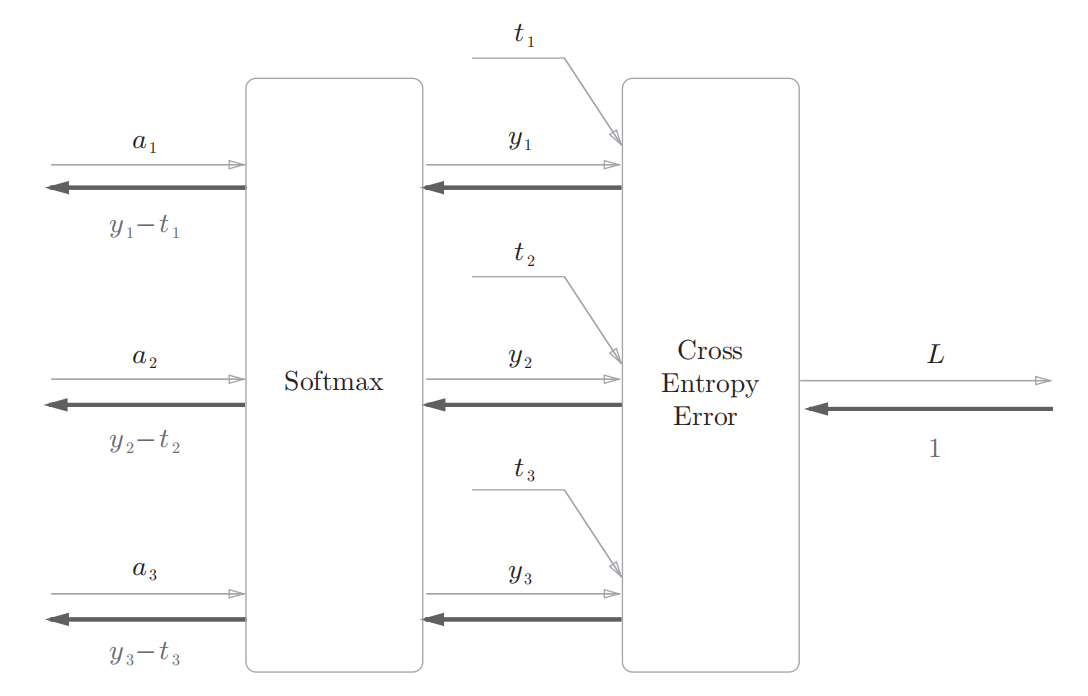
上图的计算图中，softmax函数记为Softmax层，交叉熵误差记为Cross Entropy error层。这里假设要进行三类分类，从前面的层接收三个输入，Softmax层将输入(a1,a2,a3)正规化，输出(y1,y2,y3)Cross Entropy Error层接收Softmax的输出(y1,y2,y3)和教师标签(t1,t2,t3)，从这些数据中输出损失L

上图要注意的是反向传播的结果，Softmax层的反向传播得到了(y1-t1,y2-t2,y3-t3)这样漂亮的结果。由于(y1,y2,y3)是Softmax层的输出，(t1,t2,t3)是监督数据，所以(y1-t1,y2-t2,y3-t3)是Softmax层的输出和教师标签的差分。神经网络会把这个差分表示的误差传递给前面的层。

神经网络学习的目的就是通过调整权重参数，使神经网络的输出接近教师标签。因此，必须将神经网络的输出与教师标签的误差高效地传递给前面的层

现在实现一下Softmax-with-Loss层

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class SoftmaxWithLoss:
  def __init__(self):
    self.loss = None # 损失
 		self.y = None # softmax的输出
 		self.t = None # 监督数据（one-hot vector）
 	
  def forward(self, x, t):
 		self.t = t
 		self.y = softmax(x)
 		self.loss = cross_entropy_error(self.y, self.t)
 		
    return self.loss
 
	def backward(self, dout=1):
 		batch_size = self.t.shape[0]
 		dx = (self.y - self.t) / batch_size
 r	return dx