最小二乘法的概率解释
在面对回归问题的时候,我们会思考,为什么选择线性回归,为什么选择最小二乘法成本函数 J ?在本节里会给出一系列的概率基本假设,基于这些假设,可以推出最小二乘法是一种非常自然的算法
首先假设目标变量和输入值存在下面这种等量关系
$$ y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)} $$上式中的 $\epsilon^{(i)}$ 是误差项,用于存放由于建模所忽略的变量导致的效果或者随机的噪音信息。进一步假设$\epsilon^{(i)}$是独立同分布的(IID),服从高斯分布,其平均值为0,方差为$\sigma^2$,这样就可以把这个假设写成"$\epsilon^{(i)} \sim N(0,\sigma^2)$",然后$\epsilon^{(i)}$的密度函数就是:
$$ p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(\epsilon^{(i)})^2}{2\sigma^2} \right) $$这意味着存在下面的等量关系:
$$ p(y^{(i)} \mid x^{(i)}; \theta) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) $$这里的记号 “$p(y^{(i)} \mid x^{(i)}; \theta)$“表示的是这是一个对于给定$x^{(i)}$的$y^{(i)}$的分布,用$\theta$进行了参数化,这里不能用”$p(y^{(i)} \mid x^{(i)}, \theta)$“来当作条件,因为$\theta$并不是一个随机变量,也可以将$y^{(i)}$的分布写成$y^{(i)} \mid x^{(i)};\theta \sim N(\theta^Tx^{(i)},\sigma^2)$
给定一个 $X$ 为设计矩阵,包含了全部$x^{(i)}$,然后再给定$\theta$,那么$y^{(i)}$的分布是什么?数据的概率由$p(\vec{y} \mid X;\theta)$的形式给出。在$\theta$取某个固定值的情况下,这个等式通常可以看作一个$\vec{y}$的函数。当我们把它当作 $\theta$ 的函数时,就称它为似然函数
$$ L(\theta)=L(\theta;X,\vec{y})= p(\vec{y} \mid X;\theta) $$结合之前对 $\epsilon^{(i)}$ 的独立性假设(这里对$y^{(i)}$ 以及给定的$x^{(i)}$也都做同样假设),就可以把上面这个等式改写成下面的形式
$$ \begin{aligned} L(\theta) &= \prod_{i=1}^{m} p(y^{(i)} \mid x^{(i)}; \theta) \\ &= \prod_{i=1}^{m} \left[ \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) \right] \end{aligned} $$现在,给定了 $y^{(i)}$ 和 $x^{(i)}$ 之间关系的概率模型了,用什么方法来选择咱们对参数 $\theta$ 的最佳猜测呢,最大似然法告诉我们要选择能让数据的似然函数尽可能大的 $\theta$ 。也就是说,咱们要找的 $\theta$ 能够让函数 $L(\theta)$ 取到最大值
为了运算方便,实际中我们选择最大化对数似然函数$l(\theta)$:
$$ \begin{aligned} \ell(\theta) &= \log L(\theta) \\ &= \log \prod_{i=1}^{m} \left[ \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) \right] \\ &= \sum_{i=1}^{m} \log \left[ \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) \right] \\ &= m \log \frac{1}{\sqrt{2\pi}\sigma} \;-\; \frac{1}{2\sigma^2} \sum_{i=1}^{m} (y^{(i)} - \theta^T x^{(i)})^2 \end{aligned} $$因此,对$l(\theta)$的最大值也就意味着下面这个子式取到最小值
$$ \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - \theta^T x^{(i)})^2 $$上式即为$J(\theta)$,我们最初的最小二乘成本函数
总结:在对数据进行概率假设的基础上,最小二乘回归得到的 $\theta$ 和最大似然法估计的 $\theta$ 是一致的。所以这是一系列的假设,其前提是认为最小二乘回归能够被判定为一种非常自然的方法,这种方法正好就进行了最大似然估计
还要注意,在刚才的讨论中,我们最终对 $\theta$ 的选择并不依赖 $\sigma^2$ ,而且也确实在不知道 $\sigma^2$ 的情况下就找到了结果。
局部加权线性回归
假如问题从 $x \in R$来预测 y。下面第一幅图显示了使用 $y=\theta_0+\theta_1x$来对一个数据集来进行拟合。我们明显能看出来这个数据的趋势不是一条严格的直线,所以用直线进行的拟合就不是好的方法。
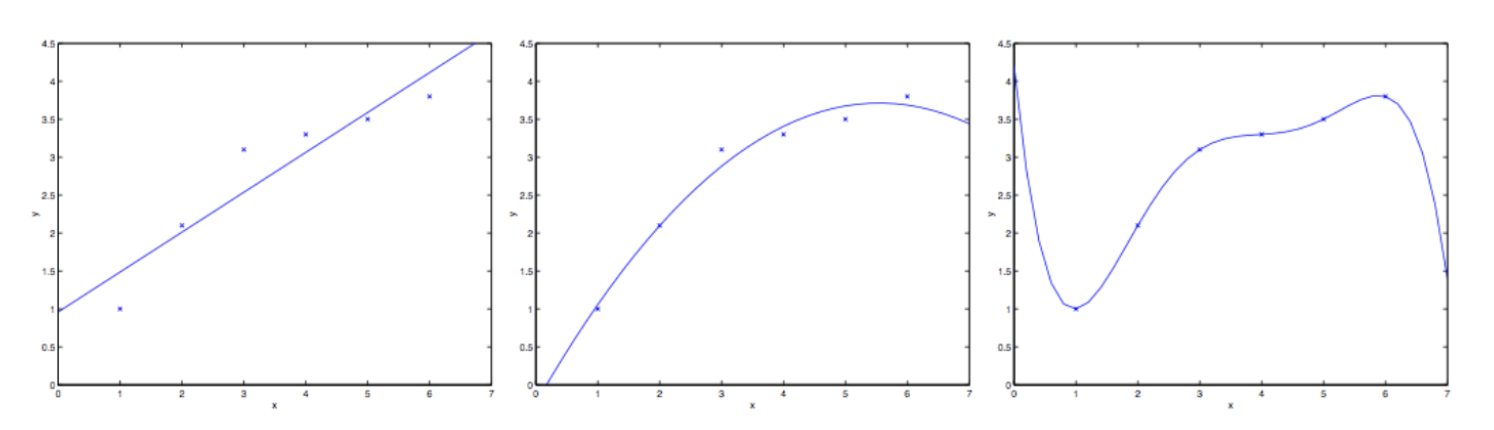
那要是我们添加一个二次项,用 $y=\theta_0 + \theta_1x + \theta_2x^2$来拟合(上面中间的图),明显如果我们对特征补充得越多,效果就越好。不过增加太多的特征也会造成危险,看第三张图就是拟合5项多项式$y=\sum_{j=0}^{5}\theta_jx^j$的结果,可以看到,虽然拟合曲线完美地通过了所有当前数据集中的数据,但我们明显不能认为这个曲线是一个合适的预测工具,比如针对不同的居住面积 $x$ 来预测房屋价格 $y$ ,左边的图是一个欠拟合的例子,明显看到漏掉了数据集中的结构信息,而最右边的图是过拟合的例子
因此,如上面例子所示,特征的选择对于确保学习算法的良好性能很重要,在本节,我们会简单地谈谈局部加权线性回归算法,这里假设有足够的训练数据,使得特征选择不那么重要
在原始版本的线性回归算法中,要对一个查询点 $x$ 进行预测,比如要衡量 $h(x)$,要经过下面的步骤:
- 使用参数 $\theta$ 进行拟合,让数据集中的值与拟合算出的值差值平方 $(y^{(i)} - \theta^Tx^{(i)})^2$最小(最小二乘法的思想)
- 输出 $\theta^Tx$
相应地,在 LWR 局部加权线性回归的方法中,步骤如下:
- 使用参数 $\theta$ 进行拟合,让加权距离$w^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2$最小
- 输出$\theta^Tx$
上面式子中的 $w^{(i)}$是非负的权值,直观地,如果$w^{(i)}$对于特定的 $i$ 很大,那么在选择 $\theta$ 时,我们将努力使 $(y^{(i)}-\theta^Tx^{(i)})$变小。如果$w^{(i)}$很小,则拟合中几乎忽略了 $(y^{(i)}-\theta^Tx^{(i)})^2$ 误差项
对于权值的选择可以使用下面这个比较标准的公式:
$$ w^{(i)}=\exp(- \frac{(x^{(i)}-x)^2}{2\tau^2} ) $$参数$\tau$控制训练样本的权重随着其$x^{(i)}$距查询点$x$的距离而下降的速度,$\tau$称为带宽参数
局部加权线性回归是我们看到的非参数算法的第一个例子。我们之前看到的(未加权)线性回归算法被称为参数算法,因为其具有固定的,有限数量的参数($\theta$),这些参数由数据拟合。一旦我们拟合了$\theta_i$并将它们存储起来,我们就不再需要保留训练数据来做出对未来的预测,相反,如果用局部加权线性回归算法,我们就必须一直保留着整个训练集,这里的"非参数"粗略的指为了呈现出假设h遂着数据集的规模大增长而线性增长,我们需要用一定顺序保存一些数据的规模
分类与逻辑回归
分类问题其实和回归问题很像,只不过我们现在要来预测的$y$的值只局限于少数的若干个离散值。首先关注的是二值化分类问题,也就是说咋们要判断的 $y$ 只有两个取值,0或者1(这里说到的大多数内容也将推广到多类情况)。例如,如果我们正在尝试为电子邮件构建垃圾邮件分类器,则 $x^{(i)}$ 可能是电子邮件的某些特征,如果是垃圾邮件,则$y$为1,否则为0。0也称为负类,1表示正类,它们有时也用符号”-“和”+“表示,给定$x^{(i)}$,相应的$y^{(i)}$也称为训练样本的标签
Logistic回归
我们可以忽略$y$是离散值的事实来处理分类问题,并使用我们的旧线性回归算法来尝试预测给定的$x$的$y$。但是,很容易构造此方法的效果非常差的例子。直觉上,当我们知道$y \in {0,1}$,所以$h_0(x)$的值如果大于1或者小于0就没有意义了,就是说$y$的值必然应当是0和1这两个值中的一个
所以咱们就改变一下假设函数$h_0(x)$的形式,来解决这个问题。比如咱们可以选择下面这个函数:
$$ h_0(x)=g(\theta^Tx)= \frac{1}{1+e^{-\theta^Tx}} $$其中有:
$$ g(z) = \frac{1}{1+e^{-z}} $$这个函数就是我们所熟悉的sigmoid函数,也叫做logistic函数,下面是它的图像
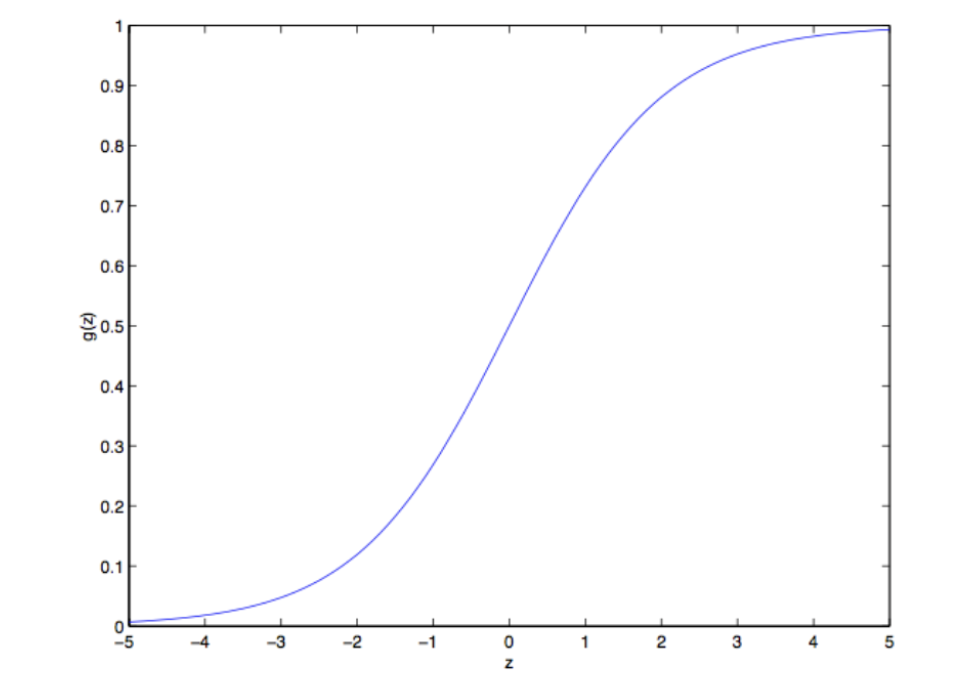
注意到,当 $z \to \infty$ 时 $g(z)$ 趋近于 1,而当 $z \to -\infty$ 时 $g(z)$ 趋近于 0。 此外,$g(z)$ 和 $h(x)$ 的值总是在 0 和 1 之间波动。 我们保持 $x_0 = 1$ 的约定,所以$\theta^T x = \theta_0 + \sum_{j=1}^{n} \theta_j x_j$
现在咱们就把 g 作为选定的函数了。当然其他的从0到1之间光滑递增的函数也可以使用,不过后面我们会了解到选择g的一些原因,对这个逻辑函数的选择是很自然的。在继续深入之前,在继续深入之前,下面通过导数讲解下这个函数的一些性质
$$ \begin{aligned} g'(z) &= \frac{d}{dz} \frac{1}{1 + e^{-z}} \\ &= \frac{1}{(1 + e^{-z})^{2}} \, (e^{-z}) \\ &= \frac{1}{(1 + e^{-z})} \left( 1 - \frac{1}{1 + e^{-z}} \right) \\ &= g(z)(1 - g(z)). \end{aligned} $$给定了逻辑回归模型了,咱们怎么去拟合一个合适的 $\theta$ 呢?我们之前已经看到了在一系列前提下,最小二乘法回归可以通过最大似然估计来推出,那么接下来就给我们这个分类模型做一系列的统计学假设,然后用最大似然法拟合参数
首先假设:
$$ P(y = 1 \mid x;\theta) = h_\theta(x) $$$$ P(y = 0 \mid x;\theta) = 1 - h_\theta(x) $$更简洁的写法是:
$$ p(y \mid x;\theta) = (h_\theta(x))^{y}\,(1 - h_\theta(x))^{1 - y} $$假设m个训练样本都是各自独立生成的,那么就可以按如下的方式来写参数的似然函数:
$$ \begin{aligned} L(\theta) &= p(\vec{y} \mid X; \theta) \\ &= \prod_{i=1}^{m} p(y^{(i)} \mid x^{(i)}; \theta) \\ &= \prod_{i=1}^{m} \left( h_\theta(x^{(i)})^{\,y^{(i)}} \, (1 - h_\theta(x^{(i)}))^{\,1 - y^{(i)}} \right) \end{aligned} $$然后和之前一样,取个对数就很容易计算最大值
$$ \begin{aligned} \ell(\theta) &= \log L(\theta) \\ &= \sum_{i=1}^{m}\Big( y^{(i)} \log h(x^{(i)}) + \big(1 - y^{(i)}\big)\log\big(1 - h(x^{(i)})\big) \Big) \end{aligned} $$怎么让似然函数最大?就跟之前在线性回归的时候用了求导数的方法类似,咱们这次就是用梯度上升法。还是写成向量的形式,然后更新,就是$\theta := \theta + \alpha \nabla_{\theta}\ell(\theta)$。(因为找最大值,所以是加号),还是先从只有一组训练样本(x,y)开始,然后求导数来退出随机梯度上升规则:
$$ \begin{aligned} \frac{\partial}{\partial \theta_j}\ell(\theta) &= \left( y \frac{1}{g(\theta^T x)} - (1-y)\frac{1}{1-g(\theta^T x)} \right) \frac{\partial}{\partial \theta_j} g(\theta^T x) \\ &= \left( y \frac{1}{g(\theta^T x)} - (1-y)\frac{1}{1-g(\theta^T x)} \right) g(\theta^T x)\bigl(1-g(\theta^T x)\bigr)\, \frac{\partial}{\partial \theta_j}\theta^T x \\ &= \Bigl( y\bigl(1-g(\theta^T x)\bigr) - (1-y)g(\theta^T x) \Bigr)\,x_j \\ &= \bigl( y - h_\theta(x) \bigr)\,x_j \end{aligned} $$上面的式子里,我们用到了对函数求导的定理$g’(z)=g(z)(1-g(z))$。然后就用到了随机梯度上升规则:
$$ \theta_j := \theta_j + \alpha\bigl(y^{(i)}-h_\theta(x^{(i)})\bigr)x_j^{(i)} $$如果我们将其和 LMS 更新规则相对比,就能发现看上去挺相似的;不过这并不是同一个算法,因为这里的$h_0(x^{(i)})$现在定义成了一个$\theta^Tx^{(i)}$的非线性函数尽管如此,我们面对不同的学习问题使用了不同的算法,却得到了看上去一样的更新规则,这是巧合吗,我们学到GLM广义线性模型的时候就会得到答案了。
题外话:感知器学习算法
现在简单聊一个算法,它的历史很有趣,并且之后讲学习理论的时候还要讲到它。设想一下,对逻辑回归方法修改一下,“强迫” 它输出的值要么是0要么是1。要实现这个目的,很自然就应该把函数 $g$ 的定义修改一下,改成一个阙值函数
$$ g(z)= \begin{cases} 1, & z \ge 0 \\ 0, & z < 0 \end{cases} $$若是我们还像之前一样令 $h_\theta(x)=g(\theta^Tx)$,但用刚刚上面的阙值函数作为 $g$ 的定义,然后如果我们用了下面的更新规则:
$$ \theta_j := \theta_j + \alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)} $$这样我们就得到了感知器学习算法
