现在是2026年01月01号的00:00,该更新note了!新年快乐!
另外一种最大化$l(\theta)$的算法
回到logistic回归,其中$g(z)$是sigmoid函数,现在让我们讨论一种最大化$l(\theta)$的不同算法
我们先想一下求一个方程零点的牛顿法。假设我们有一个从实数到实数$ f : \mathbb{R} \to \mathbb{R} $,然后要找到一个$\theta$,来满足 $f(\theta)=0$,其中$0 \in \mathbb{R}$。牛顿法就是对 $\theta$ 进行如下的更新:
$$ \theta := \theta - \frac{f(\theta)}{f'(\theta)}\tag{1} $$这个方法可以通过一个很自然的解释,我们可以把它理解成用一个线性函数来对函数 $f$ 进行逼近,这条直线是 $f$ 的切线,求解线性函数等于0的位置,并让下一个$\theta$ 的猜测为线性函数为0的地方
下面是牛顿法的图解
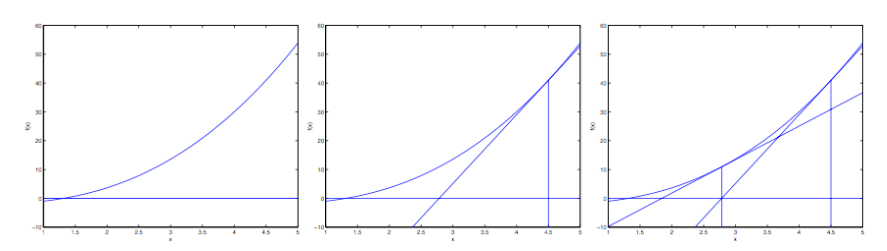
在最左边的图中,我们可以看到函数 $f$ 就是沿着 $y = 0$ 的一条直线。这时候是想要找一个 $\theta$ 来让函数值等于0,这时候发现这个 $\theta$ 值大概在1.3左右。假设我们设定初始值$\theta=4.5$。牛顿法就是在$\theta=4.5$的地方画一条切线(中间的图,这样就给出了下一个 $\theta$ 猜测值的地方,也就是这个切线的零点,大概是2.8。最右面的图中是再次进行一次这样的迭代后的结果,这时候的 $\theta$ 大概为1.8。这样多次迭代过后,很快就能接近 $\theta=1.3$
牛顿方法给出了一种求解$f(\theta)=0$的方法。如果我们想用它来最大化某些函数 $l$ 该怎么做?$l$ 的最大值对应于其一阶导数 $l’(\theta)$ 为零的点。因此,通过令 $f(\theta)=l’(\theta)$,我们可以用相同的算法来最大化 $l$,并且我们获得更新规则:
$$ \theta := \theta-\frac{l'(\theta)}{l''(\theta)}\tag{2} $$(最小化 $l$ 也是使用上述更新规则)
最后,在我们的logistic回归背景中,$\theta$ 是一个有值的向量,所以我们要对牛顿法进行扩展来适应这个情况。牛顿法进行扩展到多维情况,也叫牛顿-拉普森法(Newton-Raphson method)吗,如下
$$ \theta := \theta - H^{-1} \nabla_\theta \ell(\theta)\tag{3} $$在这里,\( \nabla \ell(\theta) \) 和往常一样,是 \( \ell(\theta) \) 关于 \( \theta_i \) 的偏导数的向量。而 \(H\) 是一个 \( n \times n \) 矩阵(实际上是\( (n+1) \times (n+1) \),假设我们包括截距项),称为 Hessian。矩阵的每一项由下式给出:
$$ H_{ij} = \frac{\partial^2 \ell(\theta)}{\partial \theta_i \, \partial \theta_j}\tag{4} $$牛顿法通常都能比(批量)梯度下降法收敛得更快,而且达到最小值所需要的迭代次数也低很多。然而,牛顿法中的单次迭代往往要比梯度下降法的单步耗费更多的性能开销,因为要查找和转换一个 \( n \times n \) 的Hessian矩阵;不过只要这个n不是太大,牛顿法通常还是更快一些。只用牛顿法来logistic回归中求似然函数 $l(\theta)$ 的最大值的时候,得到这个结果的方法叫做Fisher积分
广义线性模型
到目前为止,我们已经看到了回归样例和分类样例。在回归样例中,我们有 \( y \mid x; \theta \sim \mathcal{N}(\mu, \sigma^2) \), 在分类中, \( y \mid x; \theta \sim \text{Bernoulli}(\phi) \), \( \mu \) 和 \( \phi \) 定义为 \( x \) 和 \(\theta\) 的函数。在本节中,我们将展示这两种方法都是更广泛的模型族的特例,称为广义线性模型(GLM)。我们还将展示如何推导 GLM 族中的其他模型,并将其应用于其他分类和回归问题。
指数族
为了完成GLM,我们将首先定义指数族分布。我们说一类分布属于指数族,如果它们可以表达为如下形式:
$$ p(y; \eta) = b(y)\,\exp\!\big(\eta^{T} T(y) - a(\eta)\big)\tag{5} $$在这里,$\eta$ 称为分布的自然参数(也称为规范参数);$T(y)$是充分统计量,我们目前用的这些分布中通常 $T(y)=y$;而$a(\eta)$是一个对数分割函数。$e^{-a(\eta)}$这个量本质上扮演了归一化常数的角色,也就是确保$p(y;\eta)$的综合或者积分等于1
定义分布族的$T,a,b$由$\eta$参数化;当我们改变$\eta$的时候,我们在这个族中会获得不同的分布
现在我们看到的伯努利分布和高斯分布就都属于指数分布族。伯努利分布的均值是$ \phi $,也写作Bernoulli($ \phi $),确定的分布是$y \in {0,1}$,因此有 $p(y=1;\phi) = \phi;p(y=0;\phi)=1-\phi$。这时候只要修改$ \phi $,我们获得不同均值的伯努利分布。我们现在表明,这类伯努利分布,即通过变化$ \phi $获得的分布,是指数族;即,可以选择$T,a,b$,使得等式(5)恰好成为伯努利分布
我们现在将伯努利分布改写:
$$ \begin{aligned} p(y; \eta) &= \phi^{y}(1-\phi)^{1-y} \\ &= \exp\!\big(y \log \phi + (1-y)\log(1-\phi)\big) \\ &= \exp\!\left(\left(\log\frac{\phi}{1-\phi}\right)y + \log(1-\phi)\right) \end{aligned} $$因此,自然参数由$ \phi=log(\phi/(1-\phi)) $给出,有趣的是,如果我们翻转这个定义,用$\eta$来解 $\phi$ 就会得到 $\phi=1/(1+e^{-\eta})$。这正好就是之前我们刚刚见过的sigmoid函数!在我们把logistic回归作为一种广义线性模型(GLM)时还会遇到这个情况。
$$ \begin{aligned} T(y) &= y \\ a(\eta) &= -\log(1-\phi) \\ &= \log(1 + e^{\eta}) \\ b(y) &= 1 \end{aligned} $$上面的这组式子就表明了伯努利分布可以写成等式(6)的形式,使用一组合适的$T,a,b$
接下来继续看高斯分布。回顾一下,当推导出线性回归的时候,\( \sigma^2 \) 的值对 \(\theta\) 和 \( h(x) \) 的最终选择没有影响。因此,我们可以选择任意值的 \( \sigma^2 \) 而不改变任何东西。为了简化下面的推导,让我们令 \( \sigma^2 = 1 \),然后我们有:
$$ \begin{aligned} p(y; \mu) &= \frac{1}{\sqrt{2\pi}} \exp\!\left(-\frac{1}{2}(y-\mu)^2\right) \\ &= \frac{1}{\sqrt{2\pi}} \exp\!\left(-\frac{1}{2}y^2\right) \cdot \exp\!\left(\mu y - \frac{1}{2}\mu^2\right) \end{aligned} $$因此,我们看到高斯分布是指数族,并且有:
$$ \begin{aligned} \eta &= \mu \\ T(y) &= y \\ a(\eta) &= mu^2/2 \\ &= \eta^2/2 \\ b(y) &= (1/\sqrt{2\pi}) \exp\!\left(-y^2/2\right) \end{aligned} $$指数分布族里面还有很多其他的分布,例如多项式分布,这个待会就能看到;泊松分布,用来对计数类数据进行建模;伽马和指数分布,用于对连续的、非负的随机变量进行建 模,例如时间间隔;$\beta$ 和狄利克雷分布,用于概率的分布;还有很多,在下一节我们会描述建模型的一般方法,其中$y$(给定$ x $和$\theta$)来自任何这些分布
构造GLM
设想你要构建一个模型,来估计在给定的某个小时内来到你的商店的顾客人数(或者是你的网站的页面访问次数),基于某些确定的特征$ x $,例如商店的促销,最近的广告,天气,今天周几等等。我们已经知道泊松分布通常能适合用来对方可数目进行建模。知道了这个之后,怎么来建立一个模型来解决咱们这个具体问题呢?非常幸运的是,泊松分布是属于指数分布族的一个分部,所以我们可以使用一个广义线性模型(GLM)
更一般地,考虑一个分类或者回归问题,我们希望将某个随机变量$y$的值预测为$ x $的函数。为了得到这个问题的GLM,我们将对给定$ x $和关于我们模型的$y$的条件分布做出以下三个假设:
$y \mid x, \theta \sim \text{Exponential Family}(\eta)$,其中在给定 \( x \) 和 \(\theta\) 的条件下,\(y\) 的分布属于指数分布族,参数为 \(\eta\)。
给定$ x $,目的是要预测对应这个给定$ x $的T(y)的期望值。在我们的大多数例子中,我们有$T(y)=y$,所以着意味着我们希望我们的预测 $ h(x) $满足
$h(x) = E[y \mid x]$。(注意,这个假设通过对 $h_\theta(x)$ 的选择而满足,在逻辑回归和线性回归中都是如此。例如在逻辑回归中,
$$ h_\theta(x) = P(y = 1 \mid x; \theta) = 0 \cdot P(y = 0 \mid x; \theta) + 1 \cdot P(y = 1 \mid x; \theta) = E[y \mid x; \theta] $$)
自然参数 $\eta$ 和输入值 $ x $ 是线性相关的,$\eta = \theta^T x$,或者如果 $\eta$ 是有值的向量,则有 $\eta_i = \theta_i^T x$。
这些假设中的第三个看上去是最不和合理的假设,在我们构建GLM的方法中可能更好将其看作“设计选择”,而不是作为假设本身。这三个假设/设计选择将使我们能够得到一种非常优雅的学习算法,即GLM,它具有很多理想的属性,如易于学习。此外,得到的模型通常非常有效地用于对$y$上的不同类型的分布进行建模;例如,我们将很快展示logistic回归和普通最小二乘都可以作为GLM导出
普通最小二乘
为了表明普通最小二乘是GLM模型族的特例,考虑目标变量$y$(也称为GLM术语中的响应变量)是连续的情形,并且我们将给定的$ x $的$y$的条件分布建模为高斯分布
$$\mathcal{N}(\mu,\ \sigma^2)$$,其中$ \mu $可以是依赖$ x $的一个函数。这样,我们就让上面的指数分布族的($\eta$)分布成为了一个高斯分布。在前面的内容中我们提到过,在把高斯分布写成指数分布族的分布的时候,有$ \mu = \eta $。所以就能得到下面的等式
$$ \begin{aligned} h_\theta(x) &= E[y \mid x; \theta] \\ &= \mu \\ &= \eta \\ &= \theta^T x \end{aligned} $$第一行的等式是基于假设 2;第二个等式是基于定理:当 $ y \mid x; \theta \sim \mathcal{N}(\mu, \sigma^2) $,则 $y$ 的期望就是 $ \mu $;第三个等式是基于假设 1,以及之前我们此前将高斯分布写成指数族分布的时候推导出来的性质 $ \mu = \eta $;最后一个等式就是基于假设 3。
Logistic回归
我们现在考虑 Logistic 回归。这里我们对二元分类问题感兴趣,所以 $y \in {0, 1}$。鉴于 $y$ 是二值的,因此选择伯努利分布族来模拟给定 $ x $,$y$ 的条件分布似乎是自然的。在我们将伯努利分布表示为指数族分布时,我们得$\phi = \dfrac{1}{1 + e^{-\eta}}$。此外,请注意,如果$ y \mid x; \theta \sim \text{Bernoulli}(\phi) $,因此$E[y \mid x; \theta] = \phi$。因此,遵循与普通最小二乘法相似的推导,我们得到:
$$ \begin{aligned} h_\theta(x) &= E[y \mid x; \theta] \\ &= \phi \\ &= \dfrac{1}{1 + e^{-\eta}} \\ &= \dfrac{1}{1 + e^{-\theta^T x}} \end{aligned} $$因此,这给出了形如$h_\theta = \dfrac{1}{1 + e^{-\theta^T x}}$的假设函数。如果你以前想知道我们如何提出 logistic 函数$\dfrac{1}{1 + e^{-z}}$的形式,这给出了一个答案:一旦我们假设 $y$ 关于 $ x $ 的分布是伯努利分布,它就是 GLM 和指数族分布产生的结果。为了介绍更多的术语,给定分布的均值作为自然参数的函数$g , (g(\eta) = E[T(y); \eta])$被称为正则响应函数。它的逆$g^{-1}$ 称为正则关联函数。因此,高斯族的正则响应函数是单位函数;伯努利的正则响应函数是 logistic 函数。
Softmax回归
让我们看一下GLM的另一个例子。考虑一个分类问题,其中响应变量$y$可以取$k$个值中的任意一个,因此$y\in{1,2,…,k}$。例如,我们可能希望将电子邮件分类为垃圾邮件,个人邮件和工作相关邮件等三类,而不是将电子邮件分类为垃圾邮件或非垃圾邮件这两类。响应变量仍然是离散的,但现在可以采用两个以上的值。因此,我们将根据多项分布对其进行建模
让我们推导下GLM来建模这种多类别分类问题。为此,我们将首先将多项分布表示为指数族分布
为了在 $k$ 个可能的结果上参数化多项分布,我们可以使用 $k$ 个参数$\phi_1, \ldots, \phi_k$指定每个结果的概率。然而,这些参数将是冗余的,或者更正式地,它们将不是独立的(因为知道 $\phi_i$ 的任何 $k-1$ 个值可以唯一地确定最后一个,因为它们必须满足$\sum_{i=1}^k \phi_i = 1$)。因此,我们将仅使用 $k-1$ 个参数,$\phi_1, \ldots, \phi_{k-1}$来参数化多项分布,其中 $\phi_i = p(y = i; \varphi)$,并且$p(y = k; \varphi) = 1 - \sum_{i=1}^{k-1} p(y = i; \varphi)$。为了方便起见,我们令$\phi_k = 1 - \sum_{i=1}^{k-1} \phi_i$,但我们应该记住,这不是一个参数,而是由$\phi_1, \ldots, \phi_{k-1}$完全确定。
为了将多项分布表示为指数族分布,我们将$T(y) \in \mathbb{R}^{k-1}$定义如下:
$$ T(1)= \begin{bmatrix} 1\\0\\0\\ \vdots\\0 \end{bmatrix}, \quad T(2)= \begin{bmatrix} 0\\1\\0\\ \vdots\\0 \end{bmatrix}, \quad T(3)= \begin{bmatrix} 0\\0\\1\\ \vdots\\0 \end{bmatrix}, \ \ldots,\ T(k-1)= \begin{bmatrix} 0\\0\\0\\ \vdots\\1 \end{bmatrix}, \quad T(k)= \begin{bmatrix} 0\\0\\0\\ \vdots\\0 \end{bmatrix}. $$与我们之前的例子不同,这里我们没有$T(y) = y$;此外,$T(y)$ 现在是 $k-1$ 维向量,而不是实数。我们将用$(T(y))_i$来表示向量 $T(y)$ 的第 $i$ 个元素。
我们介绍一个非常有用的符号。如果参数为真,则示性函数$1{\cdot}$的值为 $1$,否则为 $0$,即
$$ 1\{\text{True}\} = 1,\qquad 1\{\text{False}\} = 0. $$例如,$1{2 = 3} = 0$并且$1{3 = 5 - 2} = 1$。因此,我们也可以将 $T(y)$ 和 $y$ 之间的关系写为$(T(y))_i = 1{y = i}$此外,我们有$E[(T(y))_i] = P(y = i) = \phi_i$
我们现在准备证明多项式是指数族的成员。我们有:
$$ \begin{array}{rcl} p(y;\phi) &=& \phi_1^{1\{y=1\}} \, \phi_2^{1\{y=2\}} \cdots \phi_k^{1\{y=k\}} \\[0.6em] &=& \phi_1^{1\{y=1\}} \, \phi_2^{1\{y=2\}} \cdots \phi_k^{\,1-\sum_{i=1}^{k-1} 1\{y=i\}} \\[0.6em] &=& \phi_1^{(T(y))_1} \, \phi_2^{(T(y))_2} \cdots \phi_k^{\,1-\sum_{i=1}^{k-1} (T(y))_i} \\[0.6em] &=& \exp\big((T(y))_1 \log(\phi_1) + (T(y))_2 \log(\phi_2) + \cdots + \big(1-\sum_{i=1}^{k-1} (T(y))_i\big)\log(\phi_k)\big) \\[0.6em] &=& \exp\big((T(y))_1 \log(\phi_1/\phi_k) + (T(y))_2 \log(\phi_2/\phi_k) + \cdots + (T(y))_{k-1} \log(\phi_{k-1}/\phi_k) + \log(\phi_k)\big) \\[0.6em] &=& b(y)\exp\big(\eta^T T(y) - a(\eta)\big) \end{array} $$其中
$$ \begin{aligned} \eta &= \begin{bmatrix} \log(\phi_1/\phi_k) \\ \log(\phi_2/\phi_k) \\ \vdots \\ \log(\phi_{k-1}/\phi_k) \end{bmatrix}, \\ a(\eta) &= -\log(\phi_k), \\ b(y) &= 1. \end{aligned} $$关联函数(对于 $i = 1,\ldots,k$)由下式给出:
$$ \eta_i = \log \frac{\phi_i}{\phi_k}. $$为方便起见,我们还定义$\eta_k = \log(\phi_k/\phi_k) = 0$。反转关联函数并导出响应函数,我们得到:
$$ \begin{aligned} e^{\eta_i} &= \frac{\phi_i}{\phi_k}, \\ \phi_k e^{\eta_i} &= \phi_i, \\ \phi_k \sum_{i=1}^k e^{\eta_i} &= \sum_{i=1}^k \phi_i = 1. \end{aligned} $$这意味着 $\phi_k = 1 / \sum_{i=1}^k e^{\eta_i}$,可以将其代入上式以给出响应函数
$$ \phi_i = \frac{e^{\eta_i}}{\sum_{j=1}^k e^{\eta_j}}. $$从 $\eta$ 到 $\phi$ 的映射函数称为 softmax 函数。
为了完成我们的模型,我们使用前面给出的假设 3,即 $\eta_i$ 与 $ x $ 线性相关。因此,有$\eta_i = \theta_i^T x$(对于 $i = 1,\ldots,k-1$),其中 $\theta_1,\ldots,\theta_{k-1} \in \mathbb{R}^{n+1}$ 是我们模型的参数。为了符号方便,我们还可以定义 $\theta_k = 0$, 所以 $\eta_k = \theta_k^T x = 0$,如之前所述。因此,我们的模型假设给定 $ x $,$y$ 的条件分布由下式给出:
$$ \begin{array}{rcl} p(y=i \mid x;\theta) &=& \phi_i \\[6pt] &=& \dfrac{e^{\eta_i}}{\sum_{j=1}^k e^{\eta_j}} \\[10pt] &=& \dfrac{e^{\theta_i^T x}}{\sum_{j=1}^k e^{\theta_j^T x}}. \end{array} \tag{8} $$该模型适用于分类问题,其中 $y \in {1,\ldots,k}$,称为 softmax 回归。它是 logistic 回归的推广。
我们的假设将输出
$$ \begin{array}{rcl} h_\theta(x) &=& \mathbb{E}[T(y)\mid x;\theta] \\[0.8em] &=& \mathbb{E}\!\left[\begin{array}{c} 1\{y=1\} \\ 1\{y=2\} \\ \vdots \\ 1\{y=k-1\} \end{array}\;\middle|\; x;\theta\right] \\[1.0em] &=& \begin{bmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_{k-1} \end{bmatrix} \\[1.0em] &=& \begin{bmatrix} \dfrac{e^{\theta_1^T x}}{\sum_{j=1}^k e^{\theta_j^T x}} \\ \dfrac{e^{\theta_2^T x}}{\sum_{j=1}^k e^{\theta_j^T x}} \\ \vdots \\ \dfrac{e^{\theta_{k-1}^T x}}{\sum_{j=1}^k e^{\theta_j^T x}} \end{bmatrix} \end{array} $$换句话说,对于 $i = 1,\ldots,k$ 的每个值,我们的假设将输出 $p(y=i \mid x;\theta)$ 的概率估计值。(尽管如上定义的 $ h(x) $ 仅为 $k-1$ 维,但由 $1 - \sum_{i=1}^{k-1} \phi_i$显然可以得到 $p(y=k \mid x;\theta)$。)
最后,让我们讨论参数拟合。类似于我们对普通最小二乘和 logistic 回归的原始推导,如果我们有一个训练集 ${(x^{(i)},y^{(i)}); i=1,\ldots,m}$并且想要学习这个模型的参数 $ \theta_i $,我们首先写下对数似然:
$$ \begin{array}{rcl} \ell(\theta) &=& \displaystyle \sum_{i=1}^m \log p\!\left(y^{(i)} \mid x^{(i)};\theta\right) \\[0.8em] &=& \displaystyle \sum_{i=1}^m \log \prod_{l=1}^k \left( \frac{e^{\theta_l^T x^{(i)}}} {\sum_{j=1}^k e^{\theta_j^T x^{(i)}}} \right)^{1\{y^{(i)}=l\}} \end{array} $$为了获得上面的第二行,我们使用等式 (8) 中给出的$p(y \mid x;\theta)$ 的定义。我们现在可以通过使用诸如梯度上升或牛顿法之类的方法,关于 $\theta$ 来最大化 $ \ell(\theta) $,从而获得参数的最大似然估计。
