朴素贝叶斯
在GDA中,特征向量x是连续的值为实数的向量。下面我们要讲的是当 \(x_i\) 是离散的时候所使用的另一种学习算法。
下面就来看一个样例,来尝试建立一个邮件筛选器,使用机器学习的方法。这回咱们要来对邮件信息进行分类,来判断是否为商业广告邮件还是非垃圾邮件。在学会了怎么实现之后,我们就可以让邮件阅读器能够自动对垃圾信息进行过滤,或者单独把这些垃圾邮件放进一个单独的文件夹中。对邮件进行分类是一个案例,属于文本分类这一更广泛问题集合。
假设我们有了一个训练集(也就是一堆已经标好了是否为垃圾邮件的邮件)。要构建垃圾邮件分类器,咱们先要开始确定用来描述一封邮件的特征 \(x_i\) 有哪些。
我们将用一个特征向量来表示一封邮件,这个向量的长度等于字典中单词的个数。如果邮件中包含了字典中的第 \(i\) 个单词,那么令$x_i = 1$,反之则$x_i = 0$。例如:
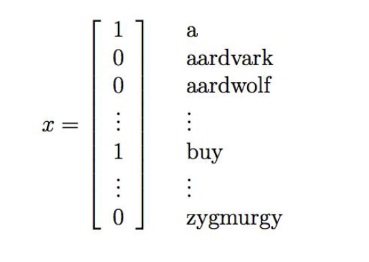
就用来表示一个邮件,其中包含了两个单词 “a” 和 “buy”,但没有单词 “aardvark”、“aardwolf” 或者 “zymurgy”。这个单词集合编码整理成的特征向量也成为词汇表,所以特征向量 x 的维度就等于词汇表的长度。
选好了特征向量了,接下来就是建立一个生成模型。所以我们必须对 $p(x \mid y)$ 进行建模。但是,假如我们的单词有五万个词,则特征向量 $x \in {0, 1}^{50000}$(即 $x$ 是一个 50000 维的向量,其值是 0 或者 1),如果我们要对这样的 $x$ 进行多项式分布的建模,那么就可能有 $2^{50000}$ 种可能的输出,然后就要用一个 $(2^{50000} - 1)$ 维的参数向量。这样参数明显太多了。
要给 $p(x \mid y)$ 建模,先来做一个非常强的假设。我们假设特征向量 $x_i$ 对于给定的 $y$ 是独立的。这个假设也叫做朴素贝叶斯假设,基于此假设衍生的算法也就叫做朴素贝叶斯分类器。
例如,如果 $y = 1$ 意味着一个邮件是垃圾邮件;然后其中 “buy” 是第2087个单词,而 “price” 是第39831个单词;那么接下来我们就假设,如果我告诉你 $y = 1$,也就是说某一个特定的邮件是垃圾邮件,那么对于 $x_{2087}$(也就是单词 buy 是否出现在邮件里)的了解并不会影响你对 $x_{39831}$(单词 price 出现的位置)的采信值。更正规一点,可以写成 $p(x_{2087} \mid y) = p(x_{2087} \mid y, x_{39831})$。(要注意这个并不是说 $x_{2087}$ 和 $x_{39831}$ 这两个特征是独立的,那样就变成了$p(X_{2087})=p(x_{2087} \mid x_{39831})$,相反,我们只假设$x_{2087}$和$x_{39831}$关于$y$条件独立)
我们现在有:
$$ \begin{array}{lcl} p(x_1, \ldots, x_{50000} \mid y) & = & p(x_1 \mid y)\, p(x_2 \mid y, x_1)\, p(x_3 \mid y, x_1, x_2)\, \ldots \, p(x_{50000} \mid y, x_1, \ldots, x_{49999}) \\ & = & p(x_1 \mid y)\, p(x_2 \mid y)\, p(x_3 \mid y)\, \ldots \, p(x_{50000} \mid y) \\ & = & \prod_{i=1}^{n} p(x_i \mid y) \end{array} $$第一个等式简单地遵循概率的通用属性,第二个等式使用 NB 假设。我们注意到,即使朴素贝叶斯假设是一个非常强的假设,所得的算法在许多问题上也能很好地工作。
我们的模型通过$\phi_{j \mid y=1} = p(x_j = 1 \mid y = 1), \phi_{j \mid y=0} = p(x_j = 1 \mid y = 0)$,以及$\phi_y = p(y = 1)$来参数化。像往常一样,给定训练集${(x^{(i)}, y^{(i)}); i = 1, \ldots, m}$,数据的似然性为:
$$ \mathcal{L}(\phi_y, \phi_{j \mid y=0}, \phi_{j \mid y=1}) = \prod_{i=1}^{m} p(x^{(i)}, y^{(i)}) $$关于 $\phi_y, \phi_{j \mid y=0}, \phi_{j \mid y=1}$ 最大化上述给出最大似然估计:
$$ \phi_{j \mid y=1} = \frac{\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1 \wedge x_j^{(i)} = 1\}} {\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1\}} $$$$ \phi_{j \mid y=0} = \frac{\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 0 \wedge x_j^{(i)} = 1\}} {\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 0\}} $$$$ \phi_y = \frac{\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1\}}{m} $$证明如下:
不难看出
$$ \begin{array}{rcl} p(y) & = & (\phi_y)^y (1 - \phi_y)^{1-y} \end{array} $$$$ \begin{array}{rcl} p(x \mid y = k) & = & \prod_{j=1}^{n} (\phi_{j \mid y = k})^{x_j} (1 - \phi_{j \mid y = k})^{1-x_j} \end{array} $$令 $\varphi$ 表示参数集
${\phi_y, \phi_{j \mid y=0}, \phi_{j \mid y=1}, j = 1, \ldots, n}$,
所以对数似然函数 $\ell(\varphi)$ 为
先关于 $\phi_{j \mid y=k}$ 求梯度
$$ \begin{array}{lcl} \nabla_{\phi_{j \mid y=k}} \ell(\varphi)& = & \sum_{i=1}^{m} \Big( x_j^{(i)} \frac{1}{\phi_{j \mid y=y^{(i)}}} \mathbf{1}\{y^{(i)} = k\}+ (1 - x_j^{(i)}) \frac{1}{1 - \phi_{j \mid y=y^{(i)}}} (-1)\mathbf{1}\{y^{(i)} = k\} \Big) \\& = & \sum_{i=1}^{m} \frac{\mathbf{1}\{y^{(i)} = k\}} {\phi_{j \mid y=y^{(i)}} (1 - \phi_{j \mid y=y^{(i)}})} \Big( x_j^{(i)} (1 - \phi_{j \mid y=y^{(i)}})- (1 - x_j^{(i)}) \phi_{j \mid y=y^{(i)}} \Big) \\& = & \frac{1}{\phi_{j \mid y=k} (1 - \phi_{j \mid y=k})} \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k\} \Big( x_j^{(i)} - \phi_{j \mid y=k} \Big) \end{array} $$令上式为0可得
$$ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k\} \big(x_j^{(i)} - \phi_{j \mid y=k}\big)= 0 \;\Rightarrow\; \left(\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k\}\right)\phi_{j \mid y=k}= \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k\} x_j^{(i)}= \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k \wedge x_j^{(i)} = 1\} \;\Rightarrow\; \phi_{j \mid y=k}= \frac{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k \wedge x_j^{(i)} = 1\} }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = k\} } $$从而
$$ \begin{array}{lcl} \phi_{j \mid y=0} & = & \displaystyle \frac{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 0 \wedge x_j^{(i)} = 1\} }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 0\} } \qquad \phi_{j \mid y=1} & = & \displaystyle \frac{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1 \wedge x_j^{(i)} = 1\} }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1\} } \end{array} $$关于 $\phi_y$ 求梯度可得
$$ \begin{array}{lcl} \nabla_{\phi_y} \ell(\varphi)& = & \displaystyle \sum_{i=1}^{m} \nabla_{\phi_y} \Big( y^{(i)} \log \phi_y+ (1 - y^{(i)}) \log(1 - \phi_y) \Big) \\& = & \displaystyle \sum_{i=1}^{m} \left( y^{(i)} \frac{1}{\phi_y}- (1 - y^{(i)}) \frac{1}{1 - \phi_y} \right) \\& = & \displaystyle \frac{1}{\phi_y (1 - \phi_y)} \sum_{i=1}^{m} \Big( y^{(i)} (1 - \phi_y)- (1 - y^{(i)}) \phi_y \Big) \\& = & \displaystyle \frac{1}{\phi_y (1 - \phi_y)} \sum_{i=1}^{m} \big( y^{(i)} - \phi_y \big) \end{array} $$令上式为 $0$ 可得
$$ \begin{array}{lcl} \phi_y & = & \displaystyle \frac{\sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1\}}{m} \end{array} $$在上面的等式中,“$\wedge$”符号表示 “and”。这些参数具有非常自然的解释。例如,$\phi_{j \mid y=1}$ 是单词 $j$ 出现在垃圾邮件($y = 1$)中的比例。在拟合了所有这些参数之后,为了对具有特征 $x$ 的新样本进行预测,我们就可以简单地进行计算
$$ \begin{array}{lcl} p(y = 1 \mid x)& = & \displaystyle \frac{p(x \mid y = 1) p(y = 1)}{p(x)}\\& = & \displaystyle \frac{ \left( \prod_{i=1}^{n} p(x_i \mid y = 1) \right) p(y = 1) }{ \left( \prod_{i=1}^{n} p(x_i \mid y = 1) \right) p(y = 1)+ \left( \prod_{i=1}^{n} p(x_i \mid y = 0) \right) p(y = 0) } \end{array} $$并选择具有较高后验概率的类别。
最后,我们注意到虽然我们已经开发了朴素贝叶斯算法,主要是针对特征 $x_i$ 是二值的问题,将其推广到 $x_i$ 可以取 ${1,2,\ldots,k_i}$ 很简单。在这里,我们只是将 $p(x_i \mid y)$ 建模为多项分布而不是伯努利分布。实际上,即使某些原始输入属性(例如,房屋的生活区域,如我们之前的示例中)是连续值,将其离散化也是很常见的,即将其转换为一小组离散值,然后应用朴素贝叶斯。例如,如果我们使用某些特征 $x_i$ 来表示生活区域,我们可以将连续值离散化如下:
| Living area (sq. feet) | < 400 | 400–800 | 800–1200 | 1200–1600 | > 1600 |
|---|---|---|---|---|---|
| $x_i$ | 1 | 2 | 3 | 4 | 5 |
因此,对于居住面积为890平方英尺的房屋,我们将相应特征 $x_i$ 的值设置为 3然后我们可以应用朴素贝叶斯算法,并使用多项分布对 $p(x_i \mid y)$ 建模,如前所述。当原始的连续值属性没有通过多元正态分布很好地建模时, 对特征进行离散化并使用朴素贝叶斯(而不是 GDA)通常会产生更好的分类器。
拉普拉斯平滑
我们已经描述过的朴素贝叶斯算法可以很好地解决许多问题,但是有一个简单的改变可以使它更好地工作,特别是对于文本分类。让我们简要讨论当前形式的算法问题,然后讨论我们如何解决它。
考虑垃圾邮件/电子邮件分类,让我们假设,在完成 CS229 并完成项目的优秀工作后,您决定在 2003 年 6 月左右将您所做的工作提交给 NIPS 会议进行发布因为您最终在电子邮件中讨论会议,所以您也开始收到带有 “nips” 字样的消息。但这是你的第一篇 NIPS 论文,直到这个时候,你还没有看到任何包含 “nips” 这个词的电子邮件;特别是 “nips” 并没有出现在你的垃圾邮件/非垃圾邮件的训练集中。假设 “nips” 是字典中的第 35000 个单词,那么你的朴素贝叶斯垃圾邮件过滤器已经选择了参数$\phi_{35000 \mid y}$ 的最大似然估计值:
$$ \begin{array}{lcl} \phi_{35000 \mid y=1}& = & \displaystyle \frac{ \sum_{i=1}^{m} \mathbf{1}\{x_{35000}^{(i)} \wedge y^{(i)} = 1\} }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1\} } = 0\\ \phi_{35000 \mid y=0}& = & \displaystyle \frac{ \sum_{i=1}^{m} \mathbf{1}\{x_{35000}^{(i)} \wedge y^{(i)} = 0\} }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 0\} }= 0 \end{array} $$即,因为它之前从未在垃圾邮件或非垃圾邮件训练样本中看到过 “nips”,它认为在任一类型的电子邮件中看到它的概率为零。因此,当试图确定这些包含 “nips” 的消息之一是否是垃圾邮件时,它会计算后验概率,并得到
$$ \begin{array}{lcl} p(y = 1 \mid x)& = & \displaystyle \frac{ \left( \prod_{i=1}^{n} p(x_i \mid y = 1) \right) p(y = 1) }{ \left( \prod_{i=1}^{n} p(x_i \mid y = 1) \right) p(y = 1)+ \left( \prod_{i=1}^{n} p(x_i \mid y = 0) \right) p(y = 0) } \\ & = & \displaystyle \frac{0}{0} \end{array} $$这是因为$\prod_{i=1}^{n} p(x_i \mid y)$中的每一项都包含$p(x_{35000} \mid y) = 0$。因此,我们的算法获得 $0/0$,并且不知道如何进行预测。
更广泛地,仅仅因为你之前没有在有限训练集中看到它,估计一些事件的概率为零在统计上是个坏主意。考虑估计取值在 ${1,\ldots,k}$ 的多项分布随机变量 $z$ 的均值问题。我们可以用$\phi_j = p(z = j)$参数化我们的多项式。给定一组 $m$ 个独立观测变量${z^{(1)}, \ldots, z^{(m)}}$,最大似然估计由下式给出
$$ \begin{array}{lcl} \phi_j& = & \displaystyle \frac{\sum_{i=1}^{m} \mathbf{1}\{z^{(i)} = j\}}{m} \end{array} $$正如我们之前看到的,如果我们使用这些最大似然估计,那么一些 $\phi_j$ 可能最终为零,这就会产生问题。为了避免这种情况,我们可以使用拉普拉斯平滑,它取代上面的估计
$$ \begin{array}{lcl} \phi_j& = & \displaystyle \frac{\sum_{i=1}^{m} \mathbf{1}\{z^{(i)} = j\} + 1}{m + k} \end{array} $$这里,我们对分子加 1,对分母加 $k$。注意$\sum_{j=1}^{k} \phi_j = 1$仍然成立。对于所有 $j$,$\phi_j \neq 0$。在某些(可以说是相当强的)条件下,可以证明拉普拉斯平滑实际上给出了 $\phi_j$ 的最优估计。
返回我们的朴素贝叶斯分类器,使用拉普拉斯平滑,我们因此得到以下参数估计:
$$ \begin{array}{lcl} \phi_{35000 \mid y=1} & = & \displaystyle \frac{ \sum_{i=1}^{m} \mathbf{1}\{x_{35000}^{(i)} \wedge y^{(i)} = 1\} + 1 }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 1\} + 2 } \\ \phi_{35000 \mid y=0} & = & \displaystyle \frac{ \sum_{i=1}^{m} \mathbf{1}\{x_{35000}^{(i)} \wedge y^{(i)} = 0\} + 1 }{ \sum_{i=1}^{m} \mathbf{1}\{y^{(i)} = 0\} + 2 } \end{array} $$