最优间隔分类器
给定一个训练集,从我们之前的讨论中可以看出,一个自然的想法是试图找到一个最大化(几何)间隔的决策边界,因为这将反映出对训练集的一个非常有信心的预测和一个对训练数据良好的“拟合”。具体而言,这将导致分类器将正和负训练样本用一个“间隙”(几何间隔)分开。
现在,假设我们得到一个线性可分的训练集;即,可以使用某个分离超平面分离正负样本。我们如何找到达到最大几何间隔的那个?我们可以提出以下优化问题:
$$ \max_{\gamma, w, b} \ \gamma $$$$ \text{s.t.} \quad y^{(i)}(w^T x^{(i)} + b) \ge \gamma, \quad i = 1, \dots, m $$$$ \|w\| = 1 $$即,我们希望最大化 $\gamma$,使得每个训练样本具有至少 $\gamma$ 的函数间隔。$|w| = 1$ 的约束确保函数间隔等于几何间隔,因此我们也保证所有几何间隔至少为 $\gamma$。因此,解决该问题将导致 $(w,b)$ 相对于训练集具有最大可能的几何间隔。
如果我们能解决上面的优化问题,我们就完成了。但是 $|w| = 1$ 约束是一个棘手的(非凸的)条件,并且这个问题肯定不是我们可以使用标准优化软件来解决的任何格式。所以,让我们尝试将问题转化为更好的问题。考虑:
$$ \max_{\hat{\gamma}, w, b} \ \frac{\hat{\gamma}}{\|w\|} $$$$ \text{s.t.} \quad y^{(i)}(w^T x^{(i)} + b) \ge \hat{\gamma}, \quad i = 1, \dots, m $$这里,我们将最大化 $\hat{\gamma}/|w|$,使得函数间隔都至少为 $\hat{\gamma}$。由于几何间隔和函数间隔的关系为 $\gamma = \hat{\gamma}/|w|$,这将给出我们想要的答案。此外,我们已经摆脱了约束 $|w| = 1$。缺点是我们仍然有一个棘手的(再次,非凸)目标函数 $\hat{\gamma}/|w|$;而且,我们仍然没有任何可以解决这种形式的优化问题的现成软件。
回想一下我们之前的讨论,我们可以在 $w$ 和 $b$ 上添加任意缩放约束而不改变任何东西。这是我们现在使用的关键想法。我们将引入缩放约束,即 $w,b$ 相对于训练集的函数间隔必须为 1:
$$ \hat{\gamma} = 1 $$由于将 $w$ 和 $b$ 乘以某个常数将导致函数间隔乘以相同的常数(这是缩放约束),并且实际上我们可以进行重新缩放 $w,b$ 的操作。对上述问题应用此性质,并注意到最大化 $\gamma/|w| = 1/|w|$ 与最小化 $|w|^2$ 相同,我们现在有以下优化问题:
$$ \min_{w,b} \ \frac{1}{2} \|w\|^2 $$$$ \text{s.t.} \quad y^{(i)}(w^T x^{(i)} + b) \ge 1, \quad i = 1, \dots, m $$我们现在已经将问题转化为可以高效解决的形式。以上是具有凸二次目标和仅有线性约束的优化问题。它的解为我们提供了最优间隔分类器。这个优化问题可以使用商业二次规划(QP)程序来解决。
虽然我们现在可以解决问题,但我们后面还是要讨论拉格朗日对偶问题。这将推导出我们的优化问题的对偶形式,它将在允许我们使用核方法(kernel)让最优间隔分类器在非常高维空间中高效运转方面发挥关键作用。对偶形式还将允许我们推导出一种有效的算法来解决上述优化问题,该优化问题通常比通用 QP 软件做得更好。
拉格朗日对偶
让我们暂时搁置 SVM 和最大间隔分类器,然后讨论如何解决约束优化问题。
考虑如下形式的问题:
$$ \min_{w} \ f(w) $$$$ \text{s.t.} \quad h_i(w) = 0, \quad i = 1, \dots, l $$在这种方法中,我们将拉格朗日算子定义为
$$ \mathcal{L}(w, \beta)= f(w)+ \sum_{i=1}^{l} \beta_i h_i(w) $$这里,$\beta_i$ 被称为拉格朗日乘子。然后我们求出 $\mathcal{L}$ 的偏导数并设为零:
$$ \frac{\partial \mathcal{L}}{\partial w_i} = 0, \qquad \frac{\partial \mathcal{L}}{\partial \beta_i} = 0 $$接着求解 $w$ 和 $\beta$。
在本节中,我们将此推广为带约束的优化问题,在这些问题中我们可能存在不等式以及等式约束。由于时间的限制,我们无法详细介绍拉格朗日二元对偶理论,但我们将给出主要思想和结果,然后应用于我们的最优间隔分类器的优化问题。
考虑以下内容,我们将其称为原始优化问题:
$$ \min_{w} \ f(w) $$$$ \text{s.t.} \quad g_i(w) \le 0, \quad i = 1, \dots, k $$$$ h_i(w) = 0, \quad i = 1, \dots, l $$为了解决这个问题,我们首先定义广义拉格朗日算子:
$$ \mathcal{L}(w, \alpha, \beta)= f(w)+ \sum_{i=1}^{k} \alpha_i g_i(w)+ \sum_{i=1}^{l} \beta_i h_i(w) $$这里,$\alpha_i$ 和 $\beta_i$ 是拉格朗日乘子。考虑
$$ \theta_P(w)= \max_{\alpha, \beta : \alpha_i \ge 0} \mathcal{L}(w, \alpha, \beta) $$这里,“$P$” 下标代表“原始”。假设给定某个 $w$。如果 $w$ 违反任何原始约束(即,对于某个 $i$,$g_i(w) > 0$ 或 $h_i(w) \neq 0$),那么可以验证
$$ \theta_P(w)= \max_{\alpha, \beta : \alpha_i \ge 0} \left( f(w)+ \sum_{i=1}^{k} \alpha_i g_i(w)+ \sum_{i=1}^{l} \beta_i h_i(w) \right) \tag{1} $$$$ = \infty \tag{2} $$相反,如果对于特定的 $w$ 确实满足约束,则 $\theta_P(w) = f(w)$。因此,
$$ \theta_P(w)= \begin{cases} f(w) & \text{如果 } w \text{ 满足原始约束} \\ \infty & \text{其他} \end{cases} $$因此,对于所有满足原始约束的 $w$,$\theta_P$ 与我们的问题中的目标具有相同的值,并且如果 $w$ 违反约束条件,那么 $\theta_P$ 为正无穷大。因此,如果我们考虑最小化问题
$$ \min_w \theta_P(w)= \min_w \max_{\alpha,\beta:\alpha_i \ge 0} \mathcal{L}(w,\alpha,\beta) $$我们看到它与我们原始的原始问题是同一个问题(即具有相同的解)。为了以后的使用,我们还将目标的最优值定义为
$$ p' = \min_w \theta_P(w) $$我们称之为原始问题的值。
现在,让我们看一个稍微不同的问题。我们定义
$$ \theta_D(\alpha,\beta)= \min_w \mathcal{L}(w,\alpha,\beta) $$这里,下标 “$D$” 代表“对偶”。还要注意,在 $\theta_P$ 的定义中,我们关于 $\alpha,\beta$ 进行了优化(最大化),而这里是关于 $w$ 的最小化。
我们现在可以提出对偶优化问题:
$$ \max_{\alpha,\beta:\alpha_i \ge 0} \theta_D(\alpha,\beta)= \max_{\alpha,\beta:\alpha_i \ge 0} \min_w \mathcal{L}(w,\alpha,\beta) $$这与上面显示的原始问题完全相同,只是现在交换了 “max” 和 “min” 的顺序。我们还将对偶问题的目标的最优值定义为
$$ d' = \max_{\alpha,\beta:\alpha_i \ge 0} \theta_D(\alpha,\beta) $$原始和对偶问题之间有什么关系?很容易证明如下这一点:
$$ d'= \max_{\alpha,\beta:\alpha_i \ge 0} \min_w \mathcal{L}(w,\alpha,\beta) \le \min_w \max_{\alpha,\beta:\alpha_i \ge 0} \mathcal{L}(w,\alpha,\beta)= p' $$事实上,我们显然有
$$ \min_w \mathcal{L}(w,\alpha,\beta) \le \mathcal{L}(w,\alpha,\beta) \le \max_{\alpha,\beta:\alpha_i \ge 0} \mathcal{L}(w,\alpha,\beta) $$从而
$$ \min_w \mathcal{L}(w,\alpha,\beta) \le \min_w \max_{\alpha,\beta:\alpha_i \ge 0} \mathcal{L}(w,\alpha,\beta)= p' $$并且
$$ d'= \max_{\alpha,\beta:\alpha_i \ge 0} \min_w \mathcal{L}(w,\alpha,\beta) \le \min_w \max_{\alpha,\beta:\alpha_i \ge 0} \mathcal{L}(w,\alpha,\beta)= p' $$但是,在某些条件下,我们会有
$$ d' = p' $$这样我们就可以解决对偶问题来代替原始问题。让我们看看这些条件是什么。
假设 $f$ 和 $g_i$ 是凸函数(即 Hessian 矩阵是正定的),$h_i$ 是仿射函数(即 $h_i(w) = a_i^T w + b$)。进一步假设 $g_i$ 约束是(严格地)可行的;这意味着存在某个 $w$ 使得对所有的 $i$ 有 $g_i(w) < 0$。
在我们的上述假设下,必将存在 $w’, \alpha’, \beta’$,使得 $w’$ 是原始问题的解,$\alpha’, \beta’$ 是对偶问题的解,而且
$$ p' = d' = \mathcal{L}(w', \alpha', \beta') $$此外,$w’, \alpha’, \beta’$ 满足 Karush-Kuhn-Tucker (KKT) 条件,如下:
$$ \frac{\partial}{\partial w_i} \mathcal{L}(w', \alpha', \beta') = 0, \quad i = 1, \dots, n \tag{3} $$$$ \frac{\partial}{\partial \beta_i} \mathcal{L}(w', \alpha', \beta') = 0, \quad i = 1, \dots, l \tag{4} $$$$ \alpha'_i g_i(w') = 0, \quad i = 1, \dots, k \tag{5} $$$$ g_i(w') \le 0, \quad i = 1, \dots, k \tag{6} $$$$ \alpha'_i \ge 0, \quad i = 1, \dots, k \tag{7} $$此外,如果某个 $w’, \alpha’, \beta’$ 满足 KKT 条件,那么它也是原始和对偶问题的解。
我们注意方程 (5),这被称为 KKT 对偶互补条件。具体来说,它推出如果 $\alpha’_i > 0$,那么 $g_i(w’) = 0$。(即,“$g_i(w’) \le 0$” 约束是有效的,这意味着它取等号而不是不等号。)稍后,这将是证明 SVM 只有少量“支持向量”的关键;当我们讨论 SMO 算法时,KKT 对偶互补条件也将为我们提供收敛性测试。
最优间隔分类器
之前,我们提出了以下(原始)优化问题来找到最优间隔分类器:
$$ \min_{w,b} \ \frac{1}{2}\|w\|^2 $$$$ \text{s.t.} \quad y^{(i)}(w^T x^{(i)} + b) \ge 1, \ i = 1, \dots, m $$我们可以将限制条件写成
$$ g_i(w) = -y^{(i)}(w^T x^{(i)} + b) + 1 \le 0 $$我们对每个训练样本都有一个这样的约束。注意,根据 KKT 对偶互补条件,我们将仅对函数间隔等于 1 的训练样本具有 $\alpha_i > 0$(即对应于取等号的约束条件,$g_i(w) = 0$)。请看下图,其中实线表示具有最大间隔分离的超平面。
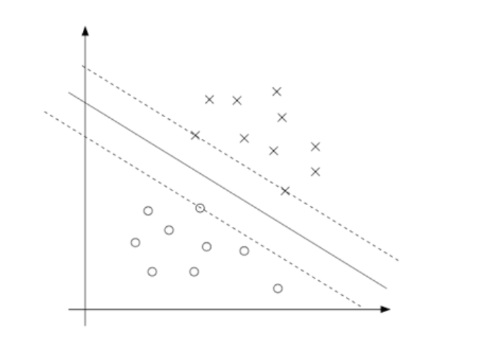
间距最小的点恰好是最接近决策边界的点;这里,这些点是平行于决策边界的虚线上三个点(一个负样本和两个正样本)。因此,在我们的优化问题的最优解中,只有三个 $\alpha_i$,即对应于这三个训练样本的 $\alpha_i$ 将是非零的。这三个点在这个问题中被称为支持向量。支持向量的数量比训练集的大小小得多的事实将在以后有用。
让我们继续。当我们推导问题的对偶形式时,需要注意的一个关键想法是我们将尝试仅根据内积 $\langle x^{(i)}, x^{(j)} \rangle$ 来编写算法(在输入特征空间中的点之间将其视为 $(x^{(i)})^T x^{(j)}$)。当我们应用内核技巧时,我们可以用这些内积来表达我们的算法,这一事实将非常关键。
当我们为优化问题构造拉格朗日算子时,我们有:
$$ \mathcal{L}(w,\alpha,\beta)= \frac{1}{2}\|w\|^2- \sum_{i=1}^{m} \alpha_i \left[ y^{(i)}(w^T x^{(i)} + b) - 1 \right] \tag{8} $$注意,只有 $\alpha_i$ 乘子而没有 $\beta_i$ 乘子,因为问题只有不等式约束。
让我们找到问题的对偶形式。为此,我们需要首先关于 $w,b$ 最小化 $\mathcal{L}(w,\alpha,\beta)$(对于固定的 $\alpha_i$),从而得到 $\theta_D$。我们通过令 $\mathcal{L}$ 关于 $w$ 和 $b$ 的偏导数为零来做到这一点。我们有:
$$ \nabla_w \mathcal{L}(w,\alpha,\beta)= w- \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)}= 0 $$这意味着
$$ w= \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)} \tag{9} $$关于 $b$ 的求导,我们得到
$$ \nabla_b \mathcal{L}(w,\alpha,\beta)= \sum_{i=1}^{m} \alpha_i y^{(i)}= 0 \tag{10} $$如果我们利用等式 (9) 中 $w$ 的定义并将其带入拉格朗日算子(等式 (8)),并简化,我们得到
$$ \mathcal{L}(w,\alpha,\beta)= \sum_{i=1}^{m} \alpha_i- \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} y^{(i)} y^{(j)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)}- b \sum_{i=1}^{m} \alpha_i y^{(i)} $$但是根据公式 (10),最后一项为 0,所以我们得到
$$ \mathcal{L}(w,\alpha,\beta)= \sum_{i=1}^{m} \alpha_i- \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} y^{(i)} y^{(j)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)} $$回想一下,通过关于 $w,b$ 最小化 $\mathcal{L}$,我们得到了上面的等式。将这与约束 $\alpha_i \ge 0$ 和约束 (10) 放在一起,我们得到以下对偶优化问题:
$$ \max_{\alpha} \quad W(\alpha)= \sum_{i=1}^{m} \alpha_i- \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle $$$$ \text{s.t.} \quad \alpha_i \ge 0, \quad i = 1, \dots, m $$$$ \sum_{i=1}^{m} \alpha_i y^{(i)} = 0 $$不难验证在我们的优化问题中确实满足 $p’ = d’$ 和 KKT 条件(等式 (3)–(7))所需的条件。因此,我们可以解决对偶问题来代替解决原始问题。具体来说,在上面的对偶问题中,我们有一个最大化问题,其中参数是 $\alpha_i$。我们稍后将讨论我们将用于解决对偶问题的特定算法,但如果我们确实能够解决它(即在满足约束条件下找到最大化 $W(\alpha)$ 的 $\alpha$),然后我们可以使用等式 (9) 返回作为 $\alpha$ 的函数的最优 $w$。找到 $w’$ 后,通过考虑原始问题,找到截距项 $b$ 的最优值也是直截了当的:
$$ b'=- \frac{ \max_{i: y^{(i)}=-1} {w'}^T x^{(i)}+ \min_{i: y^{(i)}=1} {w'}^T x^{(i)} }{2} \tag{11} $$事实上,对于 $\alpha_i \ne 0$,我们有
$$ g_i(w)=- y^{(i)}(w^T x^{(i)} + b) + 1= 0 $$所以
$$ y^{(i)}(w^T x^{(i)} + b) = 1 \quad \Longrightarrow \quad w^T x^{(i)} + b = y^{(i)} \quad \Longrightarrow \quad b = y^{(i)} - w^T x^{(i)} $$注意到
$$ g_i(w)=- y^{(i)}(w^T x^{(i)} + b) + 1 \le 0 \quad \Longleftrightarrow \quad y^{(i)}(w^T x^{(i)} + b) \ge 1 $$如果 $y^{(i)} = 1$,那么
$$ w^T x^{(i)} + b \ge 1 $$如果 $y^{(i)} = -1$,那么
$$ w^T x^{(i)} + b \le -1 $$从而满足
$$ g_i(w)=- y^{(i)}(w^T x^{(i)} + b) + 1= 0 $$的点必然为
$$ \arg \min_{i: y^{(i)}=1} w^T x^{(i)}, \qquad \arg \max_{i: y^{(i)}=-1} w^T x^{(i)} $$结合之前的式子以及最优的 $w$ 为 $w’$ 可得
$$ b= 1- \min_{i: y^{(i)}=1} {w'}^T x^{(i)}=-1- \max_{i: y^{(i)}=-1} {w'}^T x^{(i)} $$两式相加可得
$$ b'=- \frac{ \max_{i: y^{(i)}=-1} {w'}^T x^{(i)}+ \min_{i: y^{(i)}=1} {w'}^T x^{(i)} }{2} $$在继续之前,让我们更仔细地看一下等式 (9),它给出了 $w$ 的最佳值($\alpha$ 的最佳值)。假设我们已经将模型的参数拟合到训练集,现在希望在新的输入 $x$ 处进行预测。我们将计算 $w^T x + b$,并且当且仅当该项大于零时才预测 $y = 1$。但是使用 (9),这项也可以写成:
$$ \begin{align} w^T x + b&= \left( \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)} \right)^T x+ b \tag{12} \\&= \sum_{i=1}^{m} \alpha_i y^{(i)} \langle x^{(i)}, x \rangle+ b \tag{13} \end{align} $$因此,如果我们找到 $\alpha_i$,为了进行预测,我们必须计算仅取决于 $x$ 与训练集中的点之间的内积。此外,我们之前看到除了支持向量之外,$\alpha_i$ 都将为零。因此,上述求和中的许多项将为零,并且我们确实只需要找到 $x$ 和支持向量之间的内积(通常只有一小部分)就能计算 (13) 并进行预测。
通过讨论优化问题的对偶形式,我们获得了对问题结构的重要洞察,并且还能够仅根据输入特征向量之间的内积来编写整个算法。在下一节中,我们将利用属性核方法应用于我们的分类问题。由此产生的算法,支持向量机,将能够在非常高维空间中有效地学习。
