损失函数
给定一个图片数据集 ${(x_i, y_i)}_{i=1}^N$,$x_i$ 为图片,$y_i$ 为标签,损失为
$$ L = \frac{1}{N} \sum_i L_i(f(x_i, W), y_i) \tag{1} $$这是一种衡量模型预测与训练数据匹配程度的损失,我们希望这个值越低越好,这代表模型很好地拟合了训练数据
多类SVM损失
给一个$s=f(x_i,W)$
SVM损失定义为
$$ \begin{aligned} L_i &= \sum_{j \neq y_i} \begin{cases} 0 & \text{如果} s_{y_i} \ge s_j + 1 \\ s_j - s_{y_i} + 1 & \text{其他} \end{cases} \\ &= \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1) \end{aligned}\tag{2} $$SVM损失函数的形式如下
$$ L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1)\tag{3} $$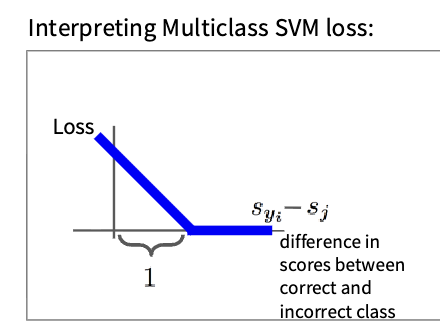
Softmax分类器
首先定义如下概率
$$ P(Y = k | X = x_i) = \frac{e^{s_k}}{\sum_j e^{s_j}} \quad s = f(x_i; W)\tag{4} $$我们想最大化对数似然函数,而这也等价于最小化如下式子
$$ L_i = -\log P(Y = y_i | X = x_i) = -\log \left( \frac{e^{s_{y_i}}}{\sum_j e^{s_j}} \right)\tag{5} $$
损失函数的正则化项
$$ L(W) = \frac{1}{N} \sum_{i=1}^{N} L_i(f(x_i, W), y_i) + \lambda R(W)\tag{6} $$它的作用是防止模型在训练数据上表现过好,因此正则化的目的就是让它在训练数据表现更差,在测试集表现更好,关于这里的$\lambda$,这是正则化强度,这也是一个超参数,这个参数用于控制模型对训练数据的拟合程度
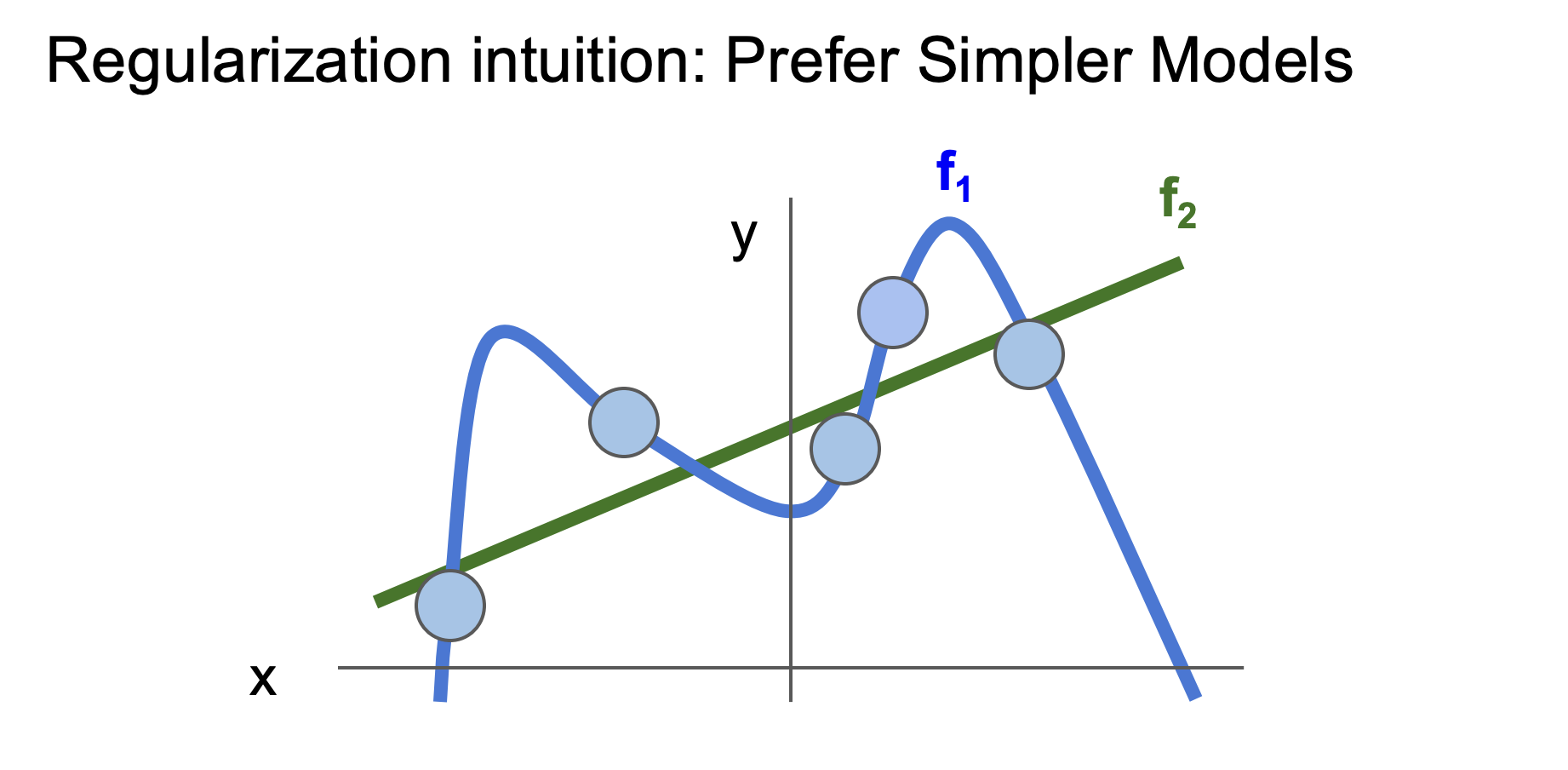
上图是一个例子,目标是拟合这些数据点,有f1和f2两种模型,f1穿过了所有数据点,所以训练或数据损失会很低,因为几乎完美拟合,但是在测试新数据上,f2可能表现更好,因此不要过度拟合数据,越简单的模型可能效果更好
比较常见的正则化项如下
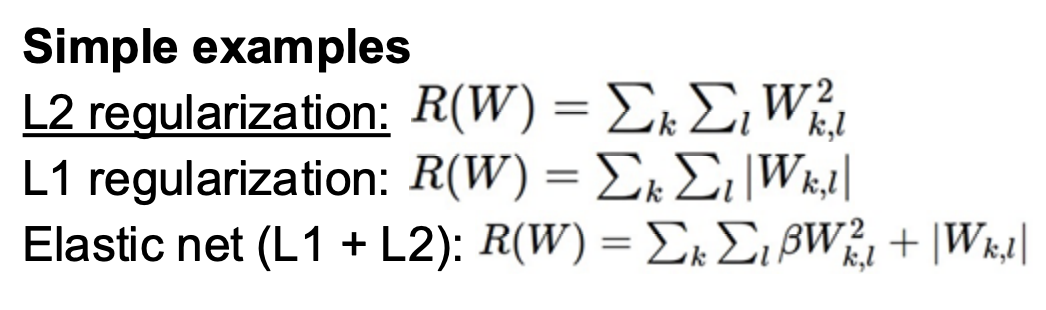
所以为什么我们要对模型正则化:
它允许我们对于权重表达某种偏好
让模型更简单从而在测试数据上表现更好
通过增加曲率改进优化
优化
梯度下降
这个我们非常熟悉了,只要跟随梯度,所以计算梯度就可以了
$$ \nabla_W L = \frac{1}{N} \sum_{i=1}^{N} \nabla_W L_i(f(x_i, W), y_i) + \lambda \nabla_W R(W)\tag{7} $$随机梯度下降(SGD)
我们之前说过可以通过遍历整个训练集,对每个i计算损失$L_i$并且汇总整个训练集,但是这样计算量太大,SGD的核心是查看一个子集代替整个训练集,每次称为一个小批量或者一批数据

但是我们会遇到一些问题,当在鞍点或者局部最优点的时候,直观点如下图
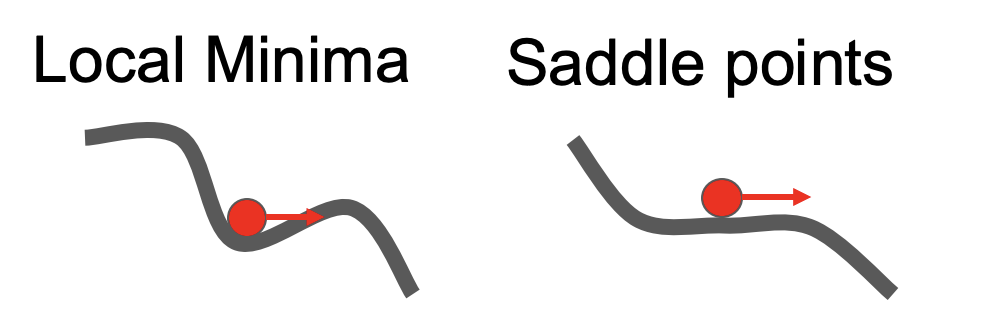
所以我们就引入了动量,你可以用高中物理学过的知识想象一下,动不了了给个动量他就能朝着预期方向继续前行

RMSProp优化器
在梯度下降中,很容易出现参数更新不稳定,也就是振荡很大的情况,RMSProp就是改进了这个问题,维护了一个梯度平方的“指数加权移动平均”,说的直白点,它可以自适应学习率,在剧烈变化的方向降低学习率
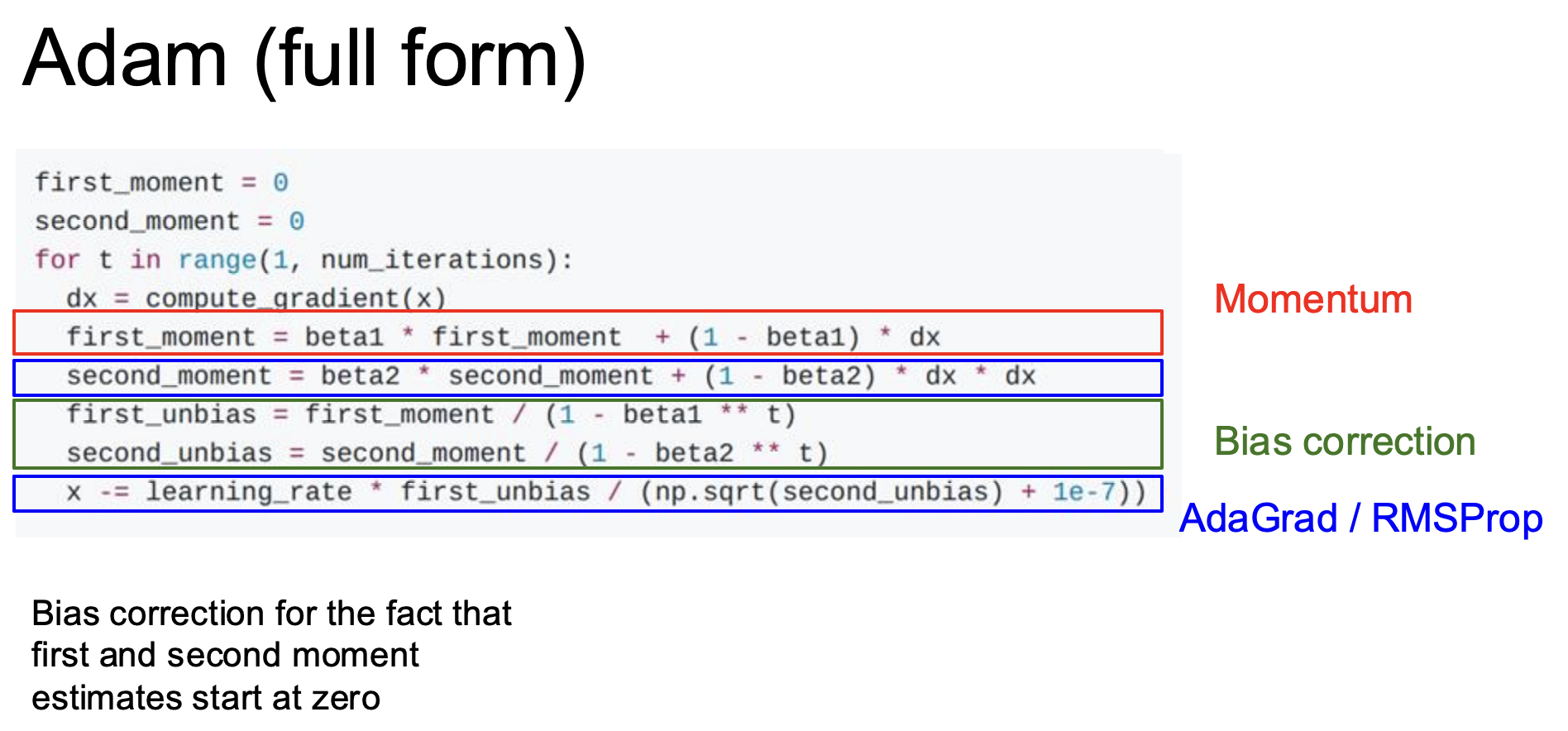
Adam优化器
Adam优化器是现在最流行的,它实际上是带动量动量的RMSProp
| |
