卷积神经网络

我们需要做的就是添加几个可以适合我们的计算图的新类型的节点，具体来说，我们只需要讨论两个运算符就可以构建更强大的网络，就是卷积层，然后是池化层，这是我们在处理图像时经常使用的另一个层

我们之前介绍的神经网络每层被称作全连接层，它是将图像的像素展平为一个大向量，进行矩阵乘法，进行ReLU，一个大问题是它破坏了图像的空间结构，比如说，图像实际上不是一维物体，是二维得到，二维结构对于这些图像的内容很重要，当你通过将原始像素拉伸称为一个大向量来构建线性分类器时，你基本上忽略了神经网络架构设计中输入数据的重要因素，所以当考虑为图像设计神经网络架构的时候，我们尤其要思考我们的网络还有哪些设计，我们可以将哪些其他计算原语插入到我们的计算图中

这就引出了卷积神经网络，所以卷积神经网络基本上是一类神经网络架构，它由线性层，非线性层，卷积层，池化层构成，有时还会将其他几个层拼接在一起形成这些神经网络架构，输入原始像素值，，然后输出图像的一些预测或者分数

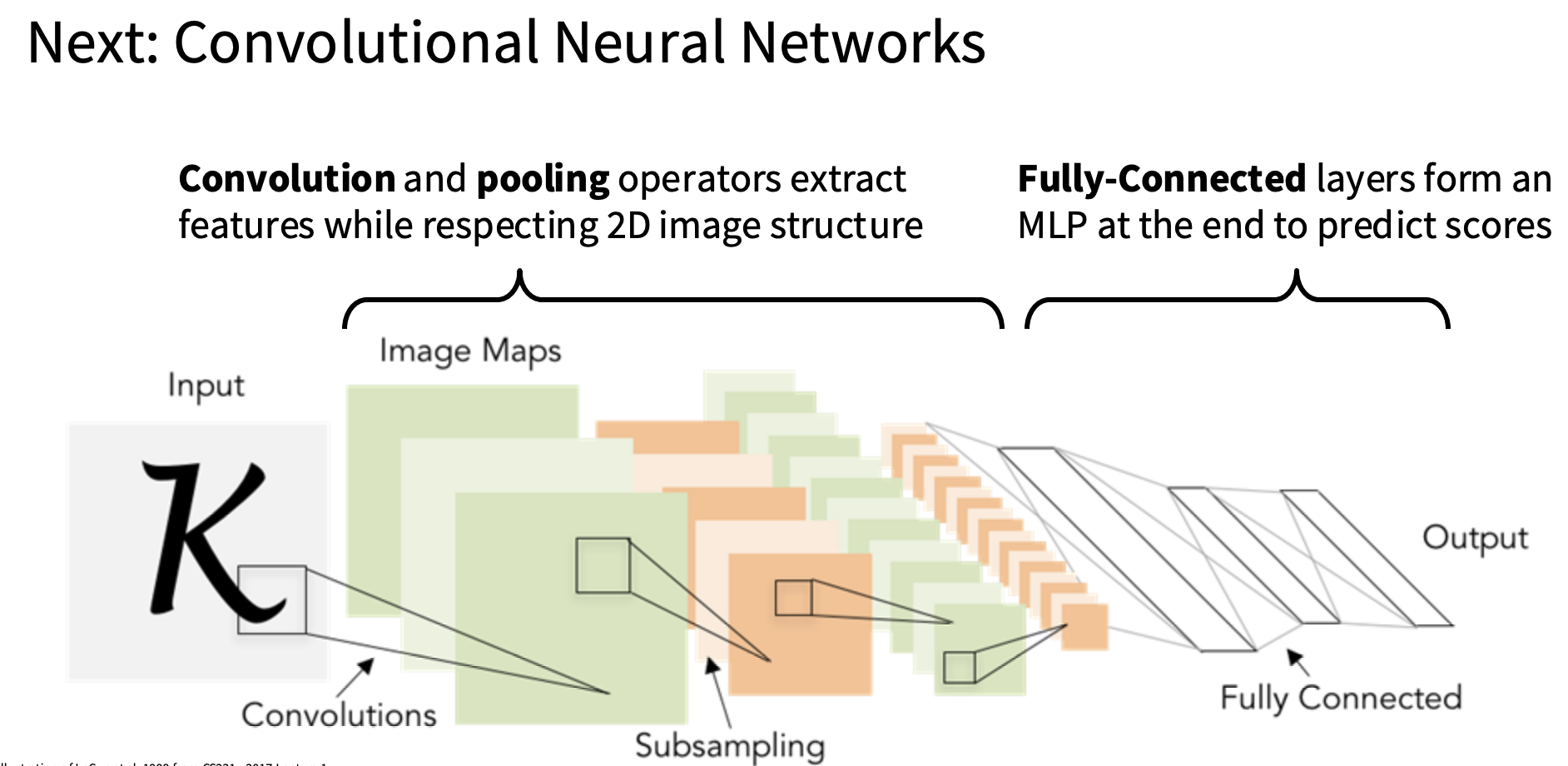
它们的一般结构通常会有一些前缀，一些网络主体，即卷积层，池化层和非线性的一些交错序列，可以被认为是为图像提取一些有用的特征表示，在此基础上，它们通常会是一些全连接层，有时候只有一层，有时候不止一层，可以将其视作多重感知器完全连接的网络分类器，它位于网络卷积部分的顶部，并从中获取特征

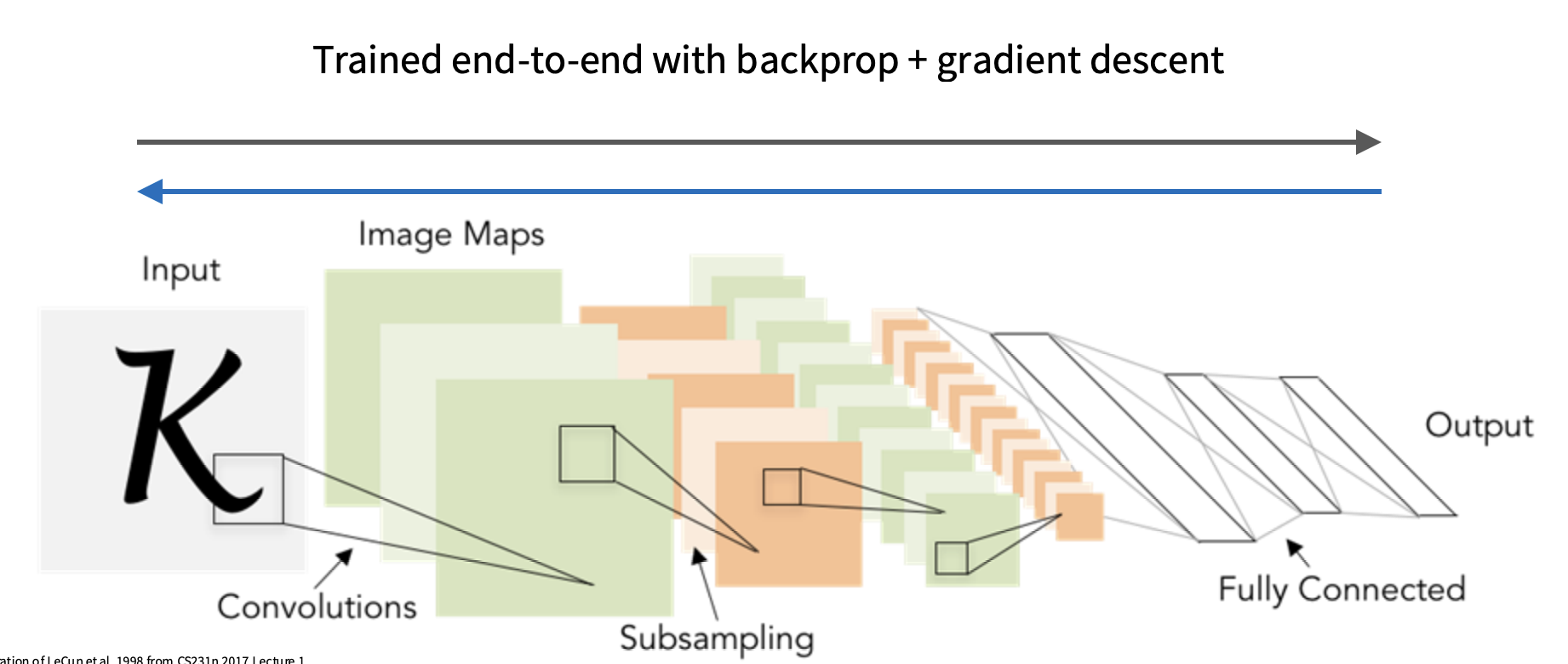
至关重要的是，通过最小化训练数据集的损失，整个系统通过梯度下降进行端到端调整

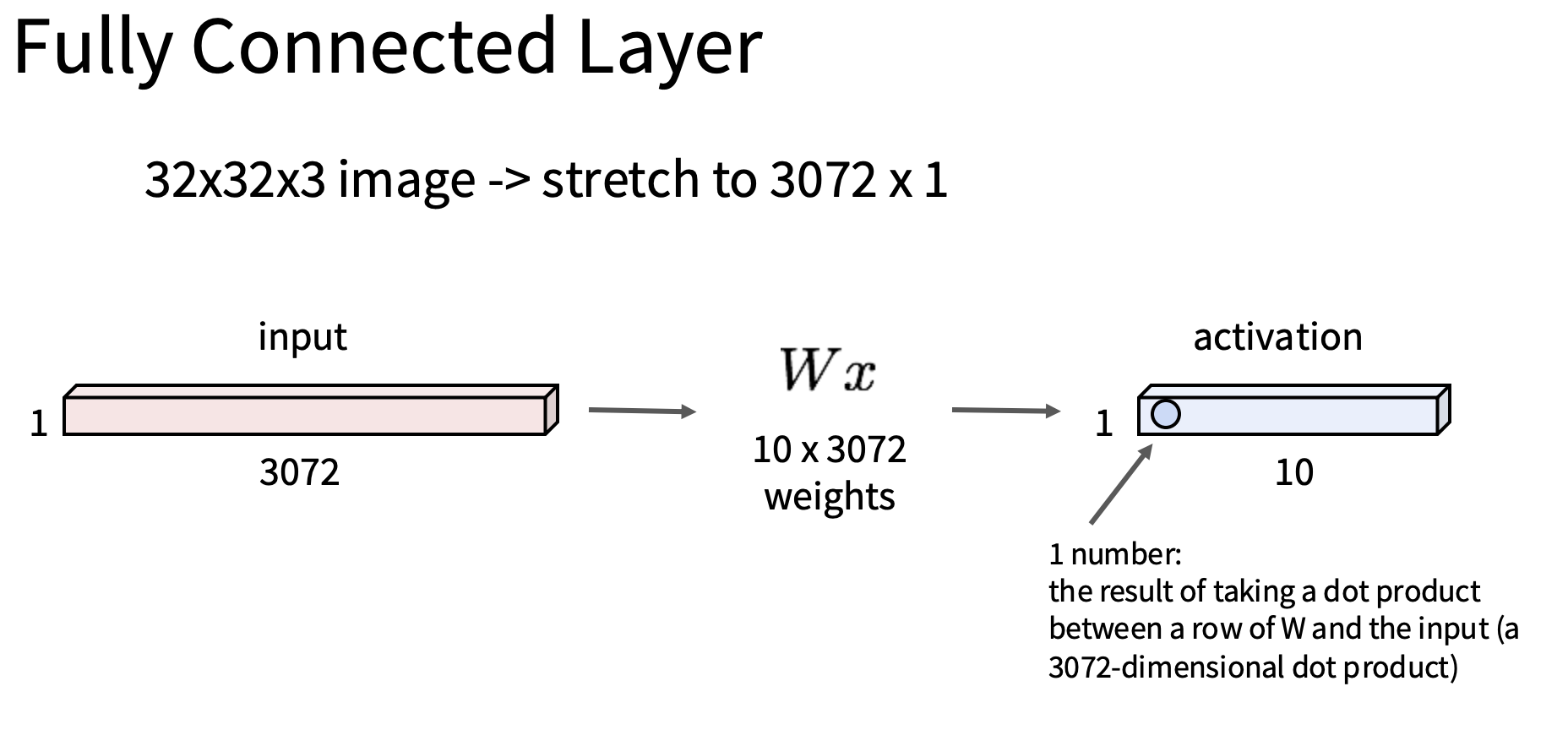
全连接层如下图

卷积层如下图

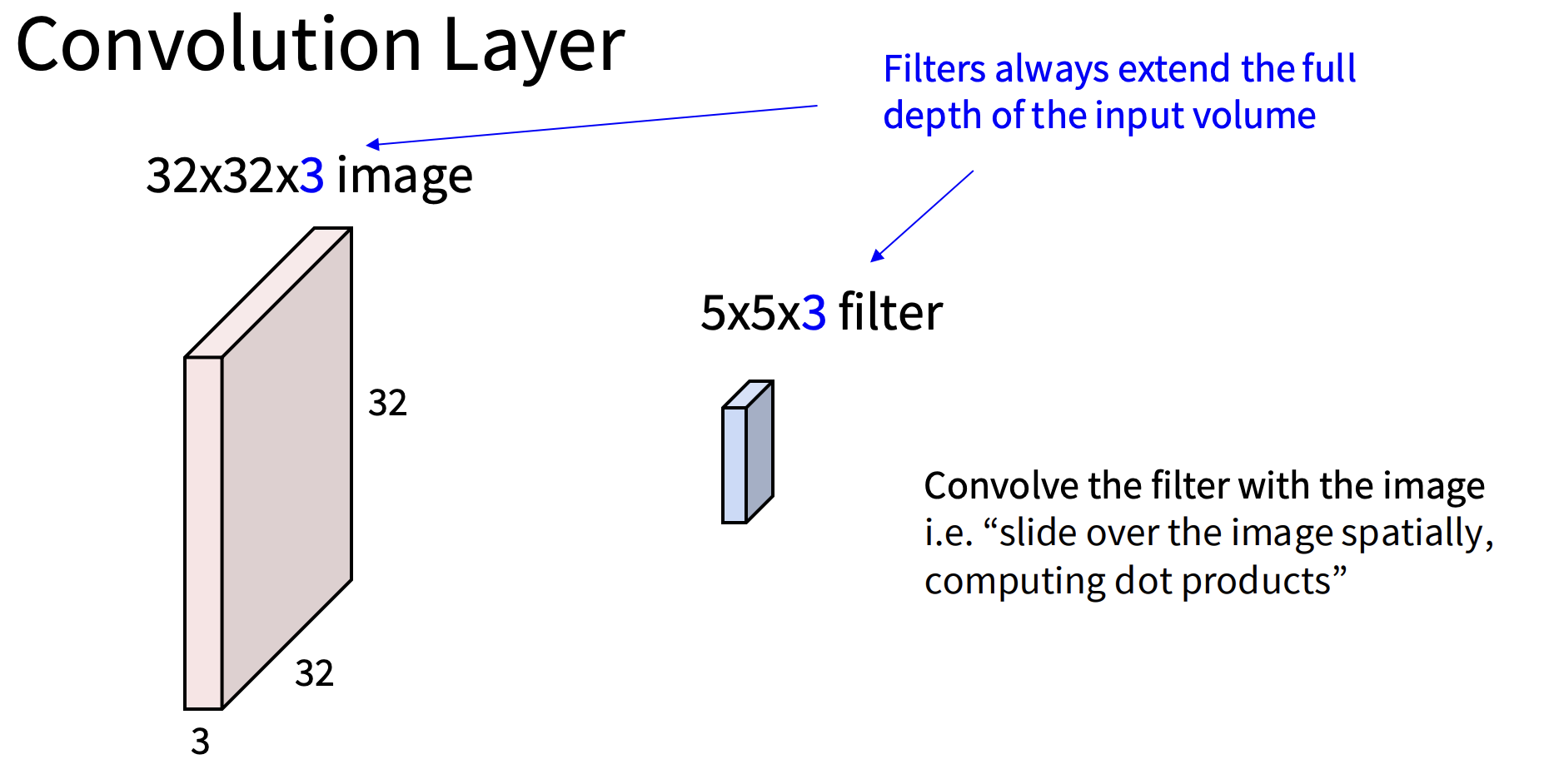
也就是说我们不会把图像拉伸成一个大向量，而是要保持图像的3D空间结构

卷积层

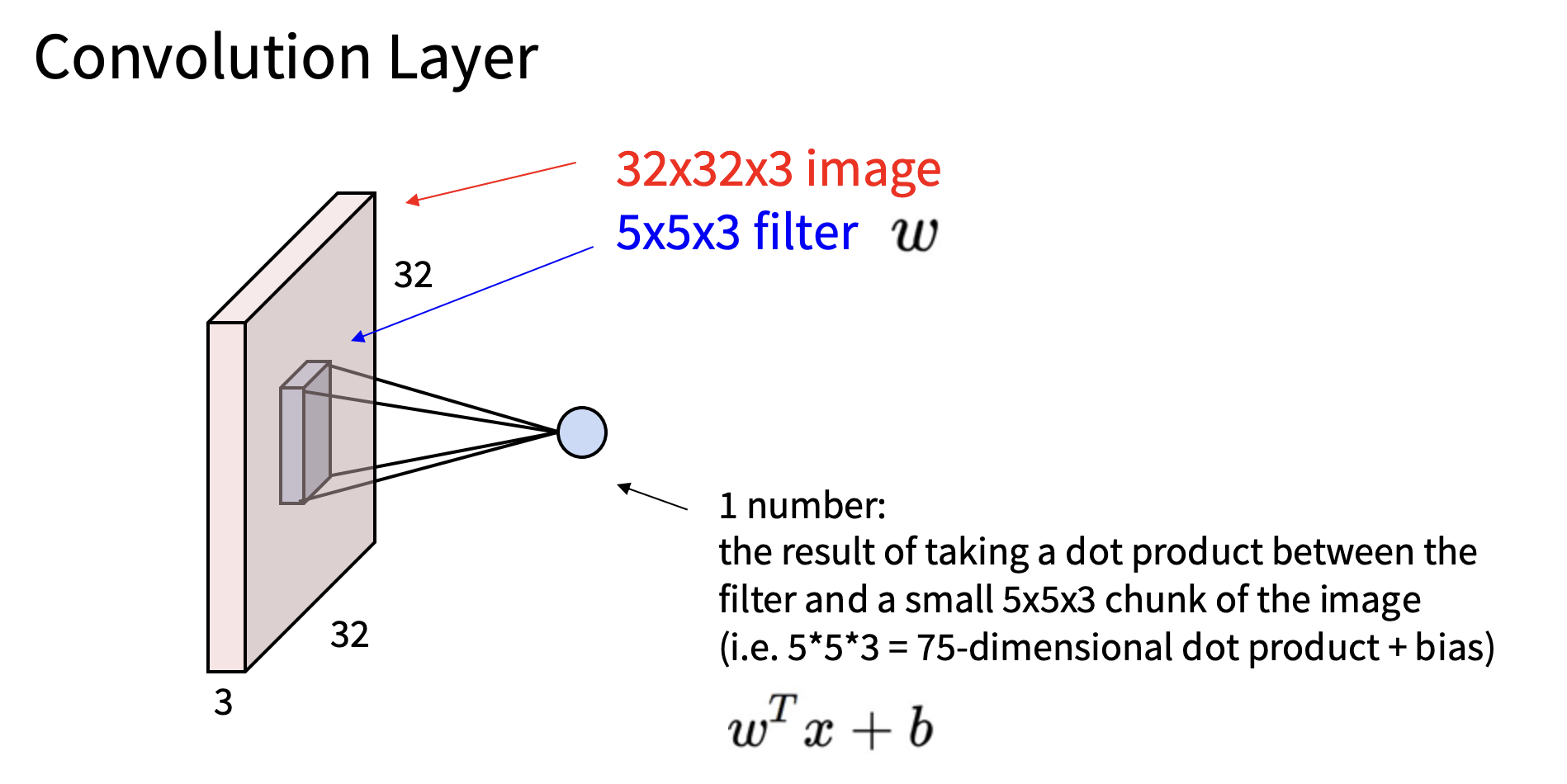
因此，如上图，我们将卷积滤波器放到图像的某个块上，这个5x5x3滤波器和该空间位置上的某个5x5x3的图像块对其，然后计算两者之间的内积，这将为我们提供一个标量数，告诉我们该图像块和模版的对齐程度

然后我们重复这个过程并且将该模块滑动到图像中的任何位置，把模版放在每个地方，我们将再次计算模版的匹配分数，该分数表示该图像部分与该模版的匹配程度，然后我们把得到的 匹配分数放在一个平面上，现在这平面是一个二维平面，基本上每个点都对应着平面上每个点与输入图像对应部分和滤波器的对齐程度

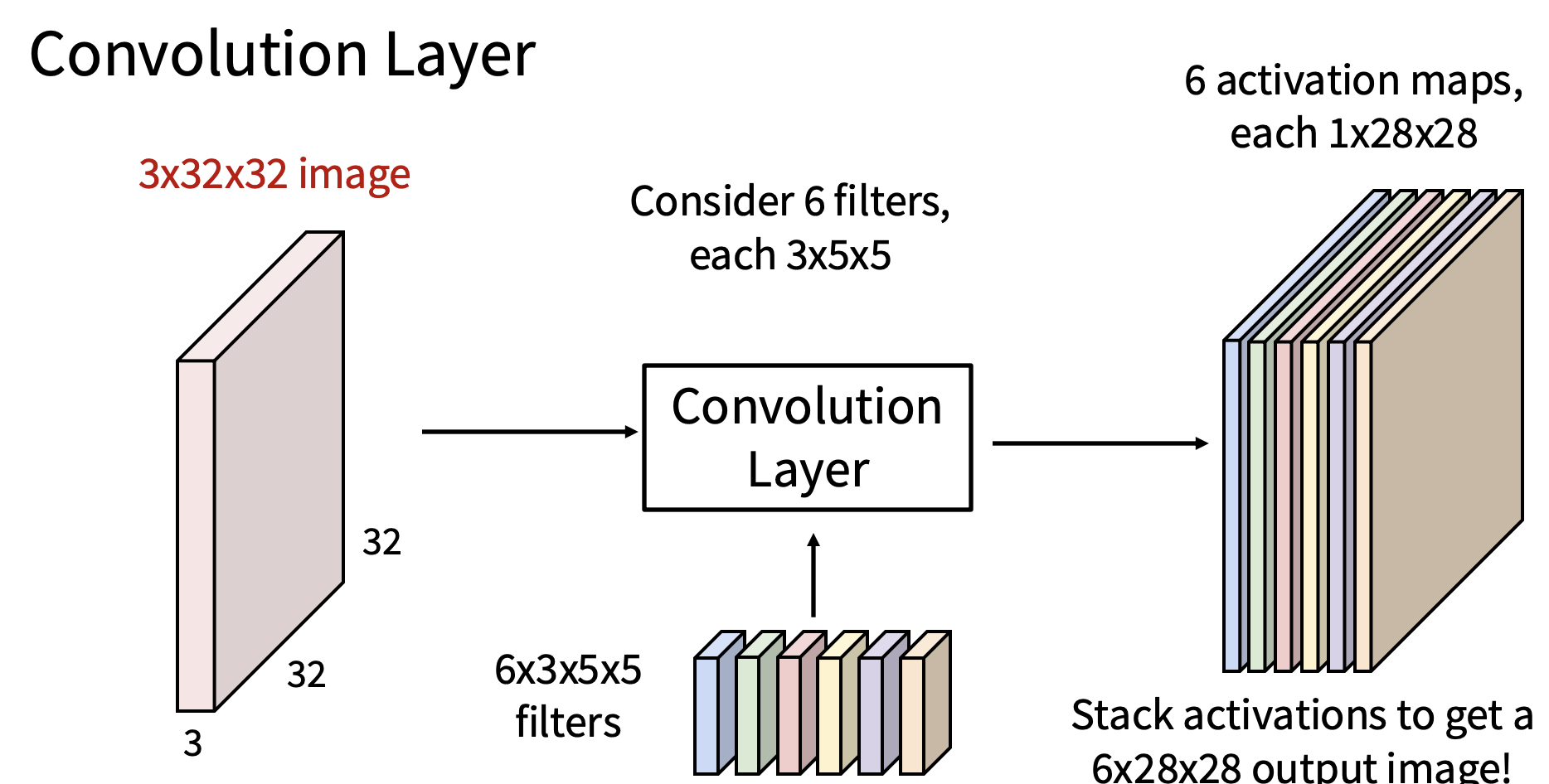
而实际中的运算我们需要多个滤波器，输出如下

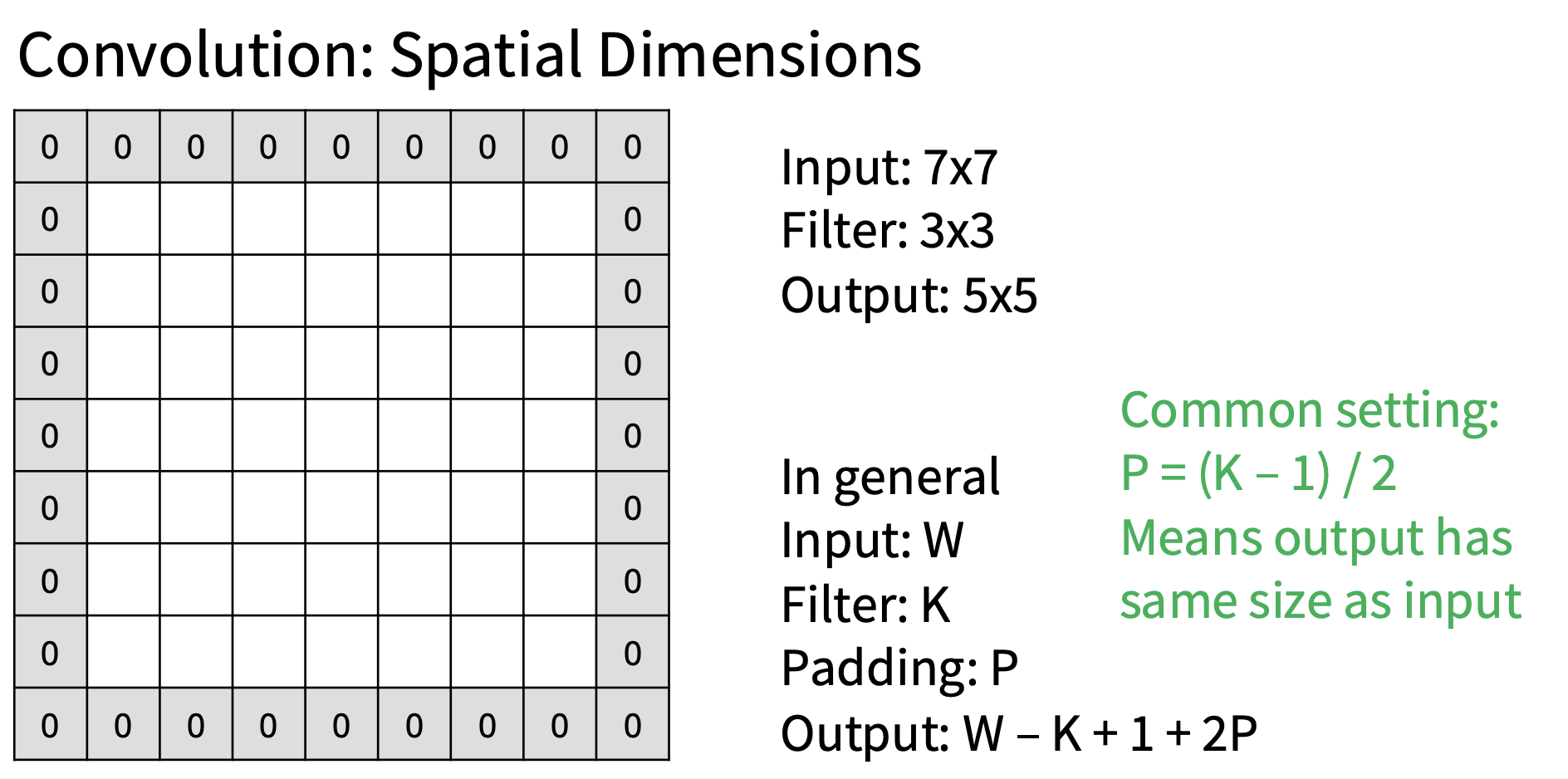
填充

在进行卷积的时候，特征图的空间尺寸会缩小，我们想让所有东西保持相同的尺寸，所以一个技巧就是填充

在计算卷积运算符之前，会在周围添加额外的零，效果如下图

感受野

在考虑单个卷积时，每个输出都在查看输入的这个局部区域，因第一层卷积的输出只能查看图像的一部分，其大小与正在学习的卷积核相同

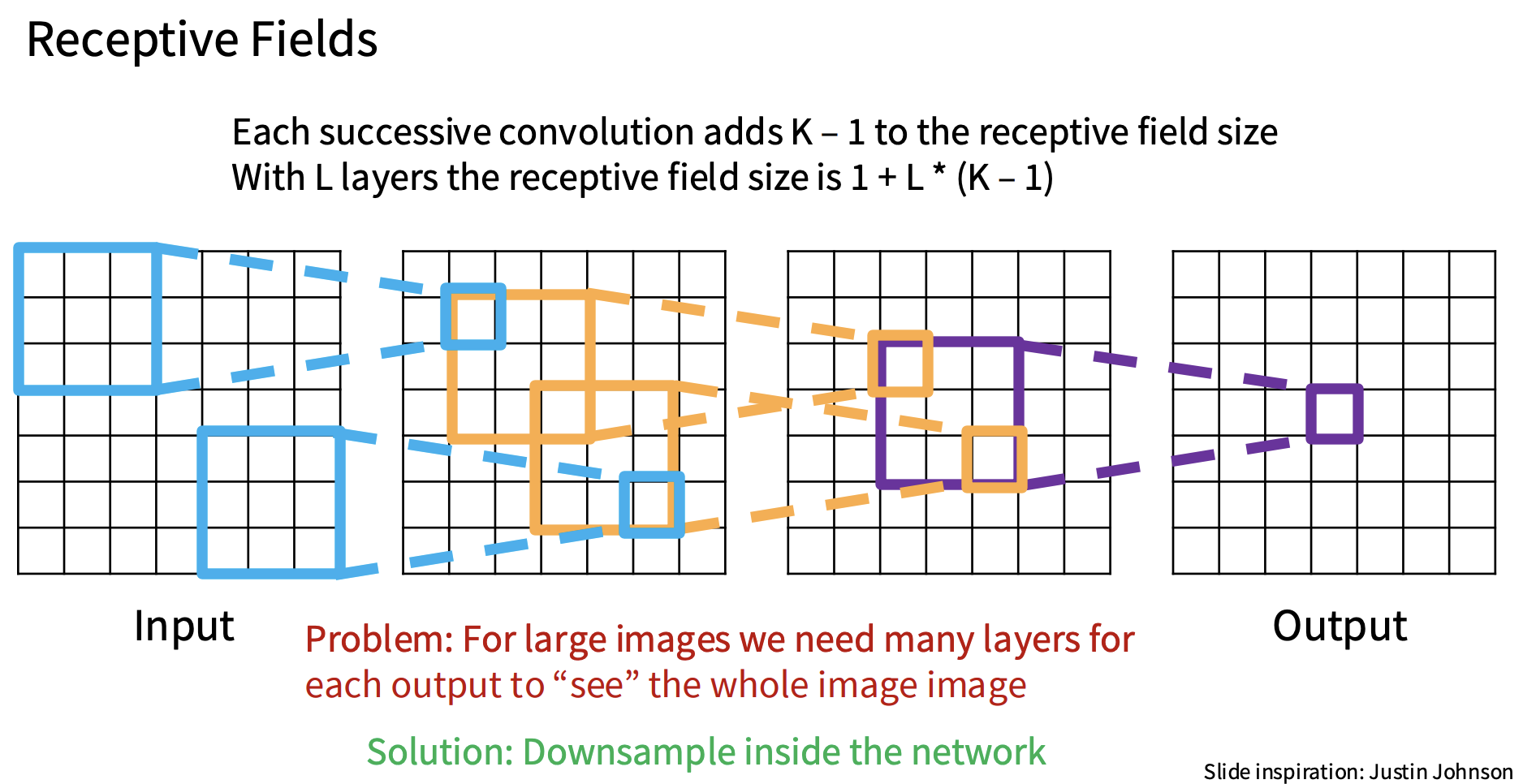
但是如果我们构建了一个将多个卷积堆叠在一起的ConvNet，如上图，这些感受野就会通过网络被放大，这里的每个条目都依赖于它之前一层的局部区域，因此，当有这些卷积时，即使每个单独的卷积都在查看它之前层中的局部邻域，当在多个层中堆叠卷积时，每个卷积所查看的原始输入的有效大小都会在网络的过程中增长，我们称之为有效感受野，所以卷积的有效感受野基本就是原始图像中有多少像素有机会影响下游网络的一次激活，这个有效感受野基本上随着卷积层的数量线性增长

有一个问题，当我们最终在网络末端做出分类决策时，我们希望我们的分类决策基本上能够汇总整个图像的全局信息，但是要很多卷积层才能做到这点，所以这里的技巧就是添加一些方法来更快增加有效感受野

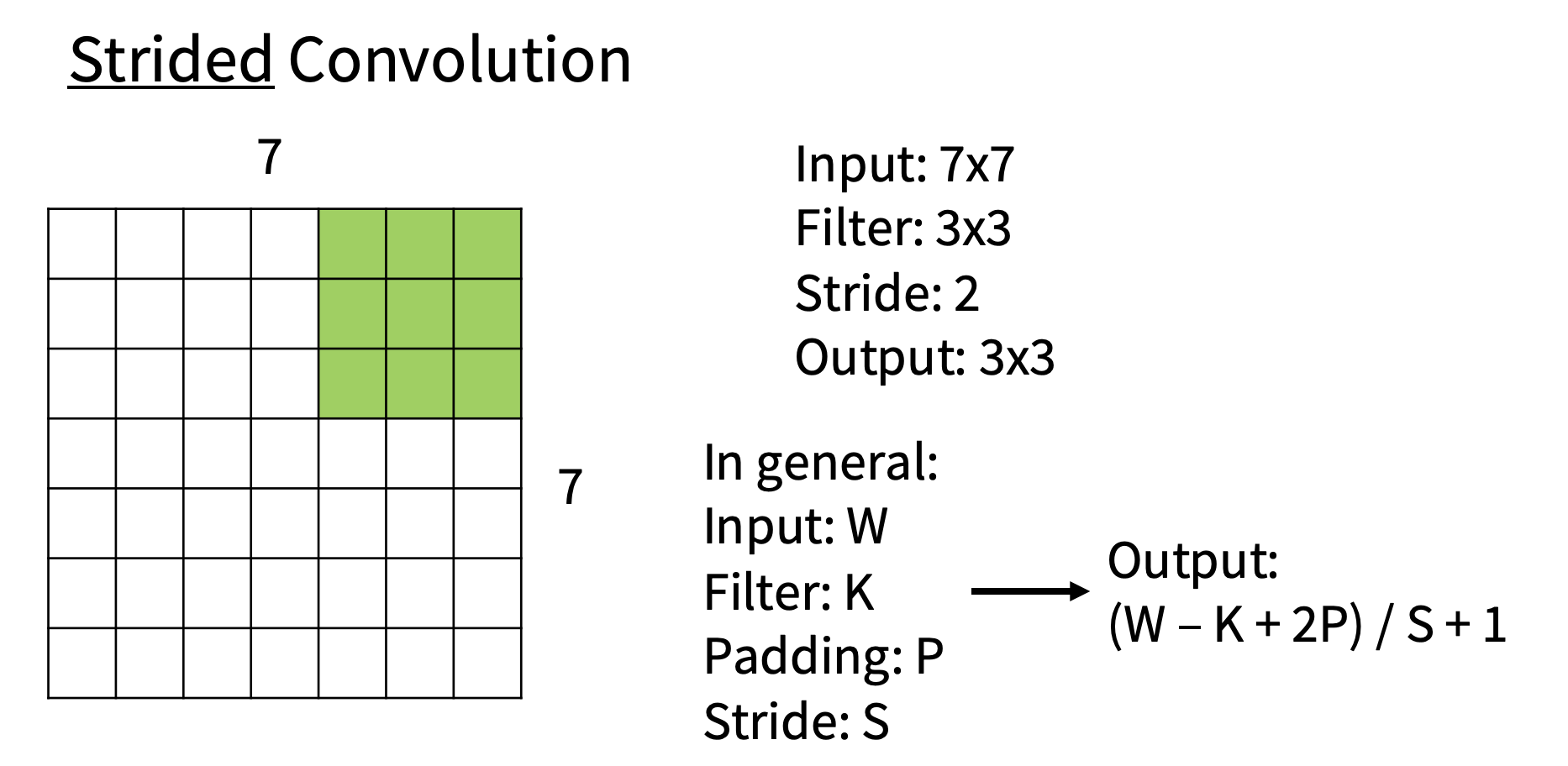
步幅

上面的例子中，我们每次移动一个单位，而实际中可以移动多个单位，每次移动的单位数量就叫做步长，记作S，输出如下

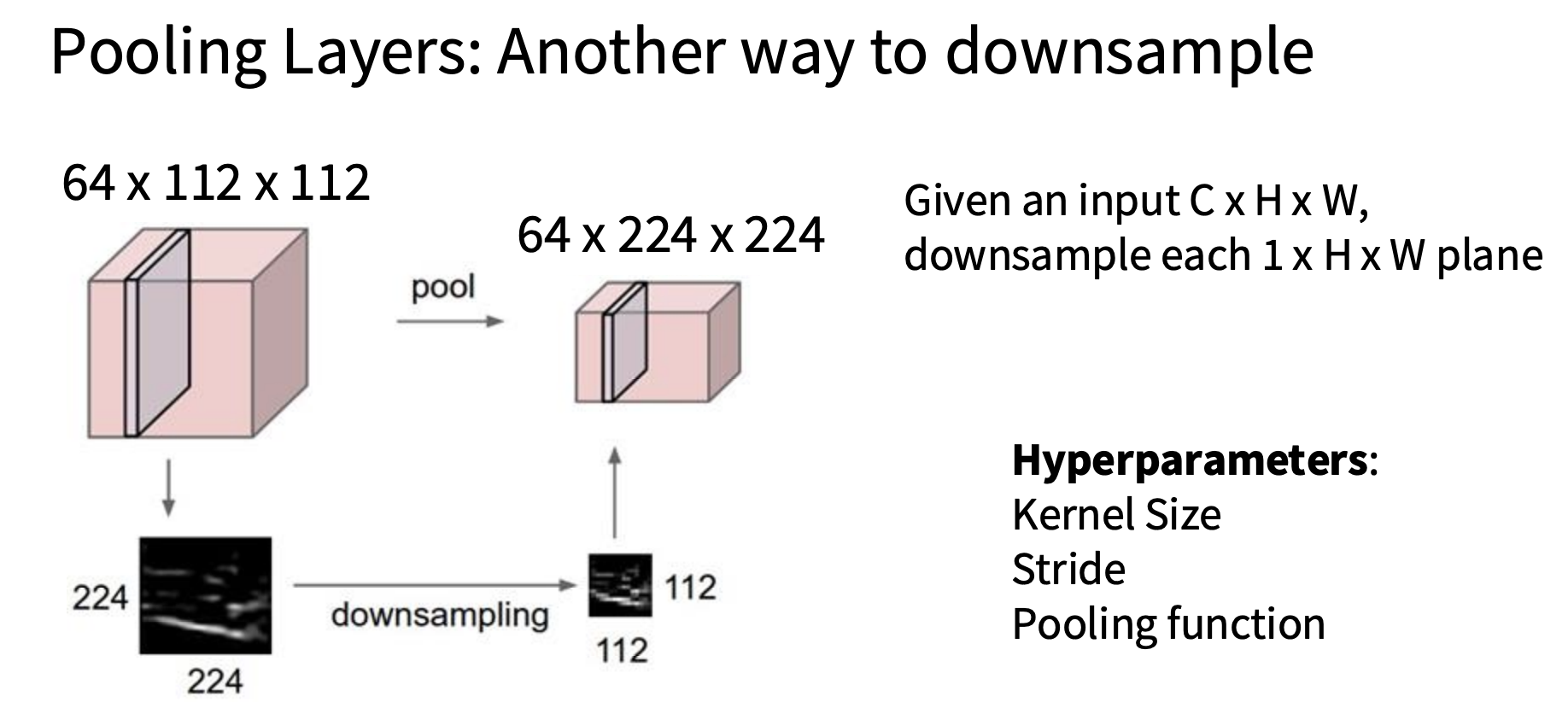
池化层

池化层基本上是神经网络内部下采样的另一种方法，因此，我们看到，步幅卷积是我们可以在神经网络内部进行下采样的一种方法，下蔡样可以让我们在深入网络时更快地建立感受场，池化层是一种廉价的下采样方法，不需要花费太多的计算。

我们采用了几种不同的下采样机制，最常用的实际上是最大值，被称为最大池化，因此，在最大池化中，我们要做的是取单个深度切片，将其划分为不重叠的区域

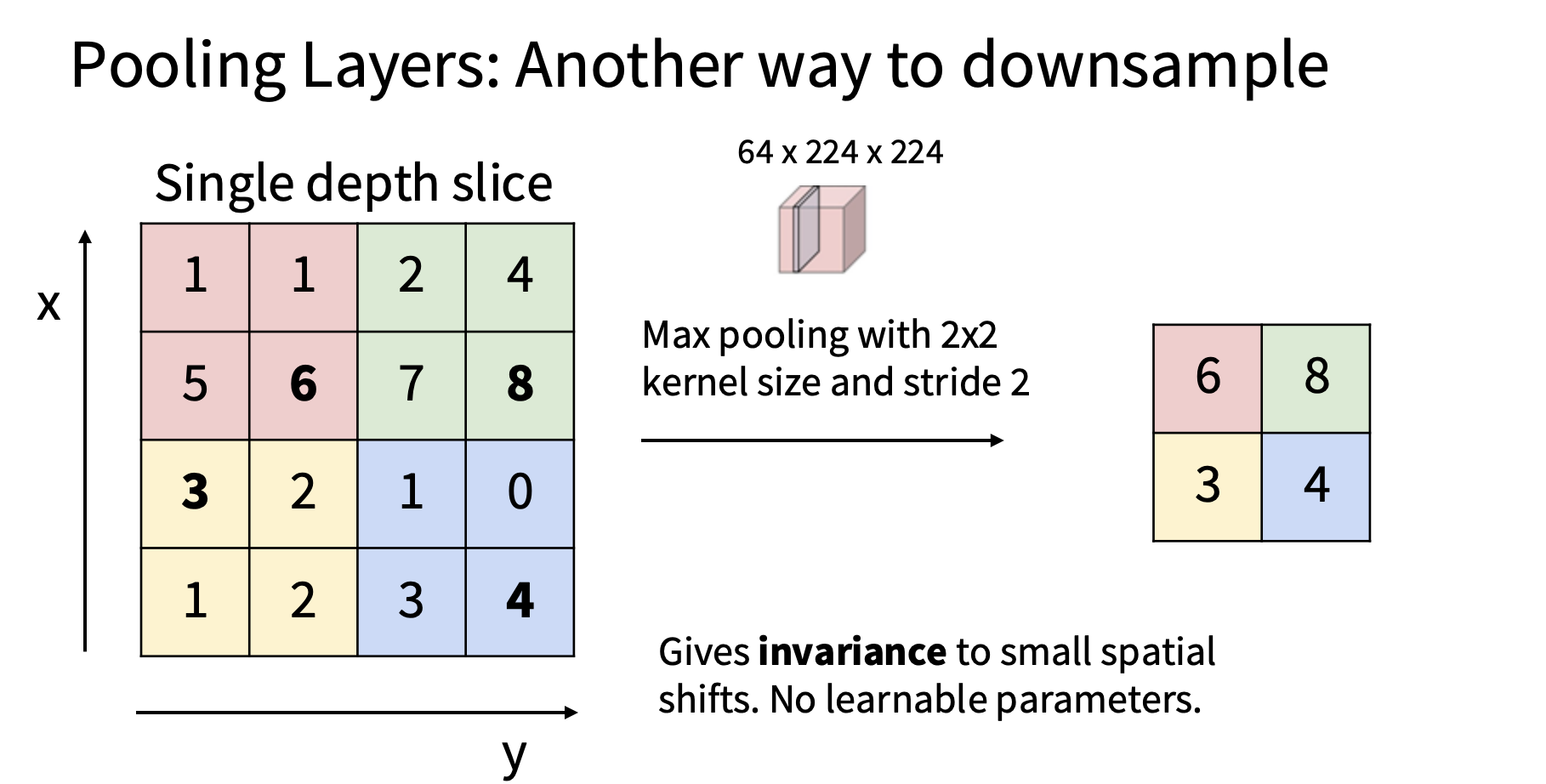
所以池化的目的是降低数据维度，图片展示的是最大值池化，实际中还有平均值池化

池化层也有对应的步长，填充参数，计算维度的方式和之前相同