CNN架构
常用的层
归一层
归一层的工作原理分为两个部分,第一步是将输入数据归一化为标准正态分布,均值为0,标准差为1,然后进行缩放和偏移,通过乘以某个值调整中心偏差,再进行偏移以改变均值位置,所有归一化层都采用这样的技术,它们之间的区别在于如何计算统计量,均值和标准差,以及将这些统计量应用到哪些值
层归一化
这是最常用的归一化层,如下图

下面的图片展示了几种不同的归一化方法和它们各自张量的哪些维度上计算均值和方差
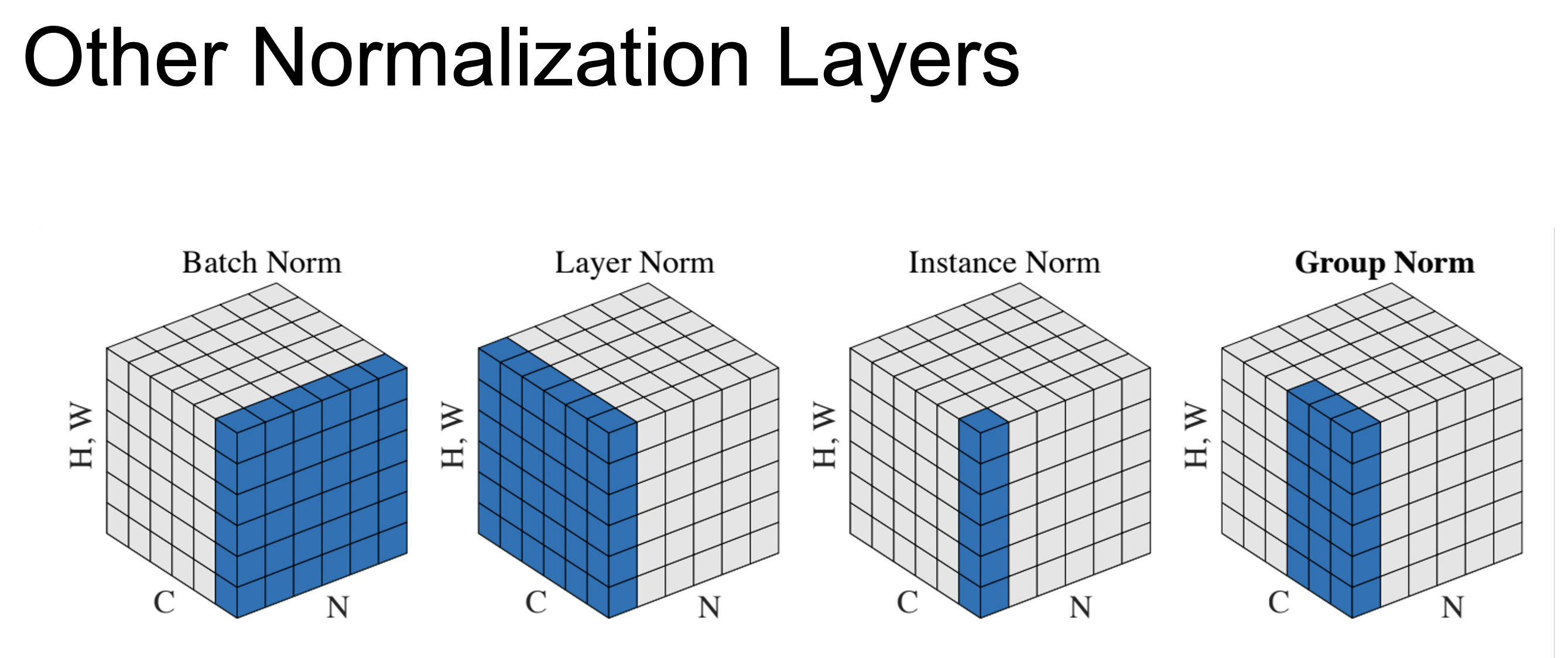
Dropout层
Dropout层的核心思想是在训练时添加随机性,而在测试时移除,目的是让模型难以过拟合训练数据,但会提升泛化能力,具体实现如下图,我们实际上随机将某些输出或激活值归零
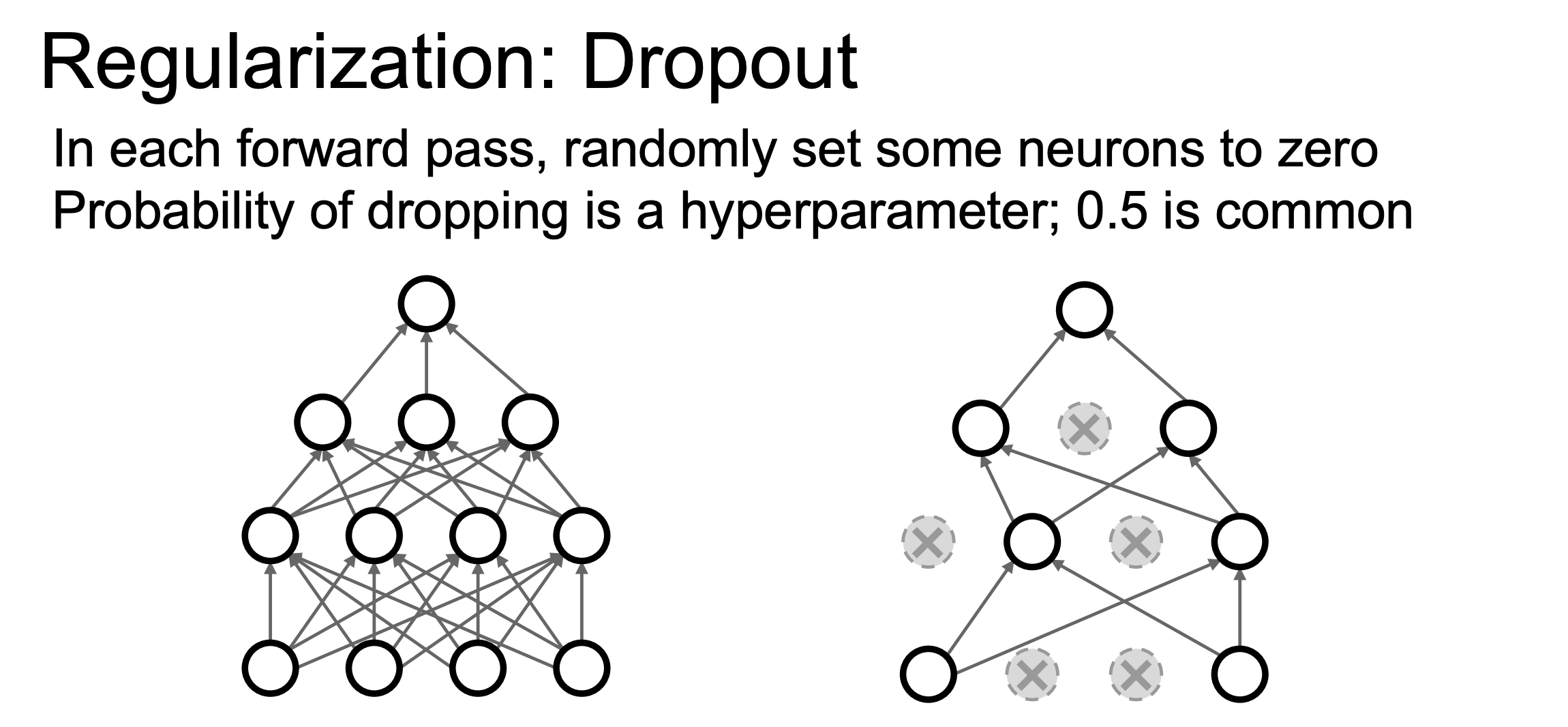
下面是伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| """ Vanilla Dropout: Not recommended implementation (see notes below) """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
""" X contains the data """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) < p # second dropout mask
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
out = np.dot(W3, H2) + b3
|
上述方法需要注意一点:在预测的时候要乘以dropout概率$p$,这是因为假设输入为$x$,其期望输出为$px$,所以为了保持一致,预测时要乘以dropout概率$p$。这要会产生一个问题:预测时增加了运算量,一个改进方式如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| """
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
H2 = np.maximum(0, np.dot(W2, H1) + b2)
out = np.dot(W3, H2) + b3
|
激活函数
激活函数的核心作用是为模型引入非线性
sigmoid函数
sigmoid函数的表达式如下
$$
\sigma(x)=1/(1+e^{-x})
$$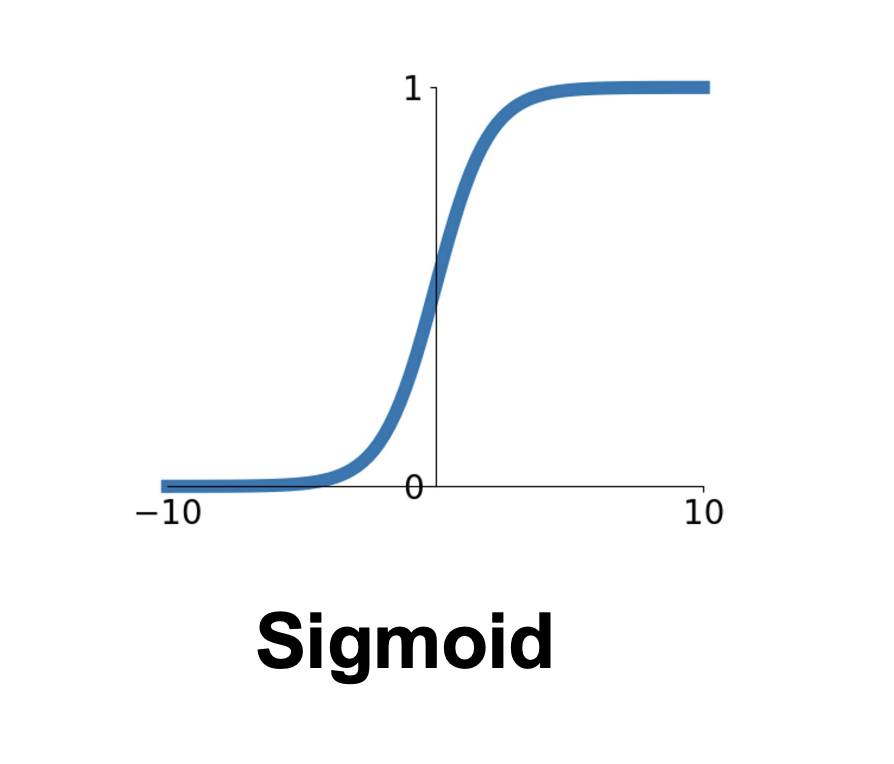
sigmoid函数主要有以下的问题:
- 经过多层sigmoid后,反向传播时梯度会越来越小
- 由于Sigmoid函数输出结果都大于0,由乘法门的含义可知,这会导致梯度的符号都相同,这也不利于训练。
ReLU
ReLU的表达式如下
$$
f(x)=max(0,x)
$$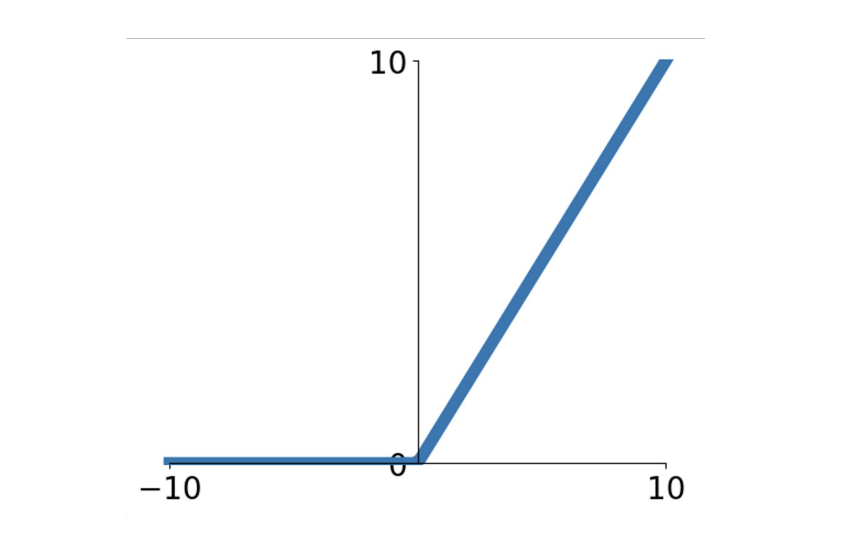
ReLU在正区域不会出现梯度消失的情况,但是在负区域还是会出现梯度为0的情况,所以我们基本上覆盖了输入域的一半,这个肯定比sigmoid函数牛逼,并且只需要计算0和x的最大值也比sigmoid函数效率更高
但是还是有上面的问题,对于任何负输入,会得到零梯度
GELU
GELU的表达式如下
$$
f(x)=x*\phi(x)
$$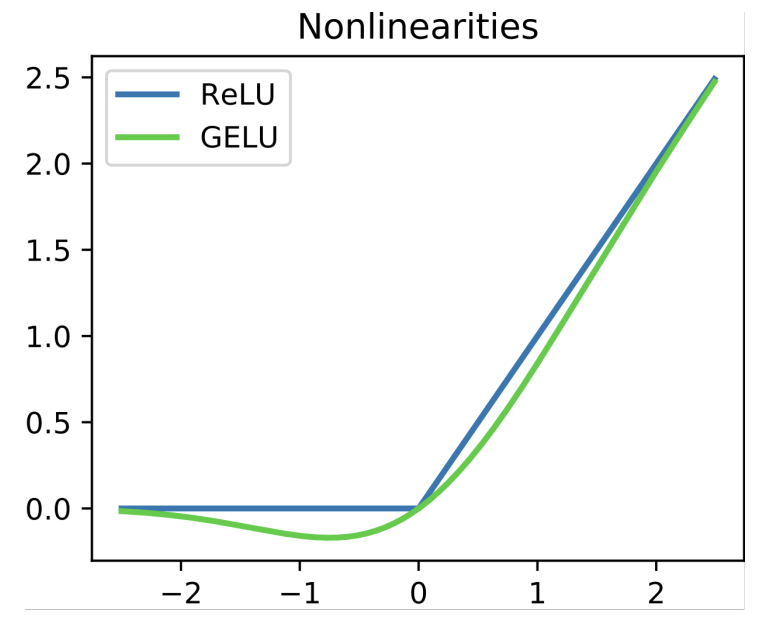
GELU在接近零的邻域内保留激活函数的非平坦区域,核心思想就是平滑0处的非连续跳跃
那么这些CNN中的激活函数在哪里用
答:通常放在线性算子之后(比如全连接层,卷积层)
残差网络
如果在普通CNN网络上不断堆叠更深的层,不断叠加新层,让网络变得越来越大,会发生什么年?
他们发现二十层模型的测试误差实际上低于56层模型,你可能会认为这是过拟合导致的,但是其实当我们看训练误差,20层模型的训练误差也更低,如下图
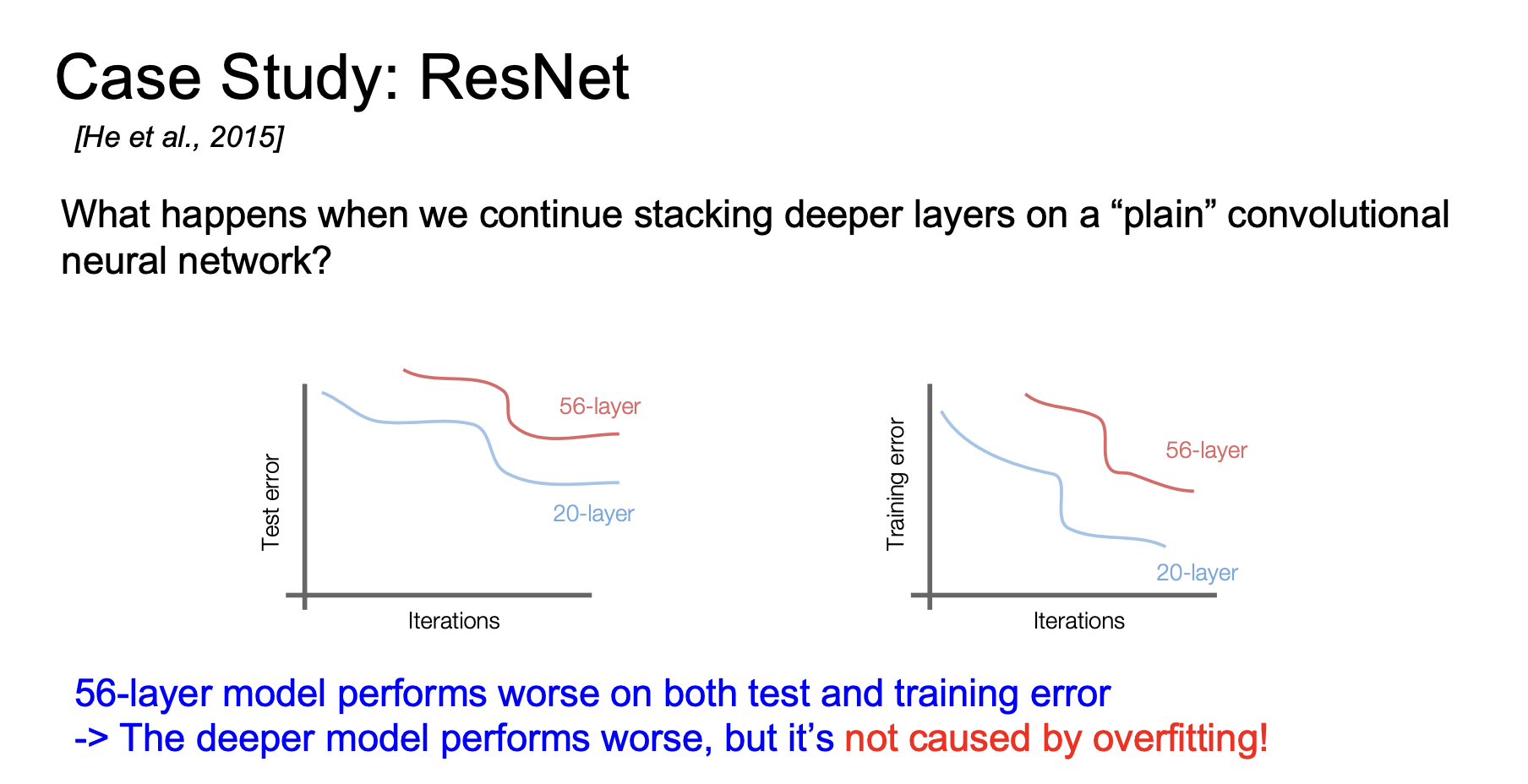
所以为什么会56层模型表现不如20层模型,更深的模型有更强的表示能力,理论上它们能表示浅层网络能处理的所有模型,因此可能的输入与输出之间的映射关系对于大型网络时小型网络的超集,因为从理论上讲,你可以想象将某些层设置为恒等函数,这些层不做任何操作,如果你将一半的层设置为无操作,你拥有的表示能力与模型完全相同,大小减半,所以说不是这些模型更差,但在表示能力方便,它们实际上更难优化,因为深层网络的可能模型集合更大,并且包含所有浅层网络可能学习到的模型

那么深层模型如何至少与浅层模型一样好,如下图,我们有一个一层模型和一个两层模型,如果我们让其中一个层几乎成为单位矩阵,模型至少应该和浅层模型一样好
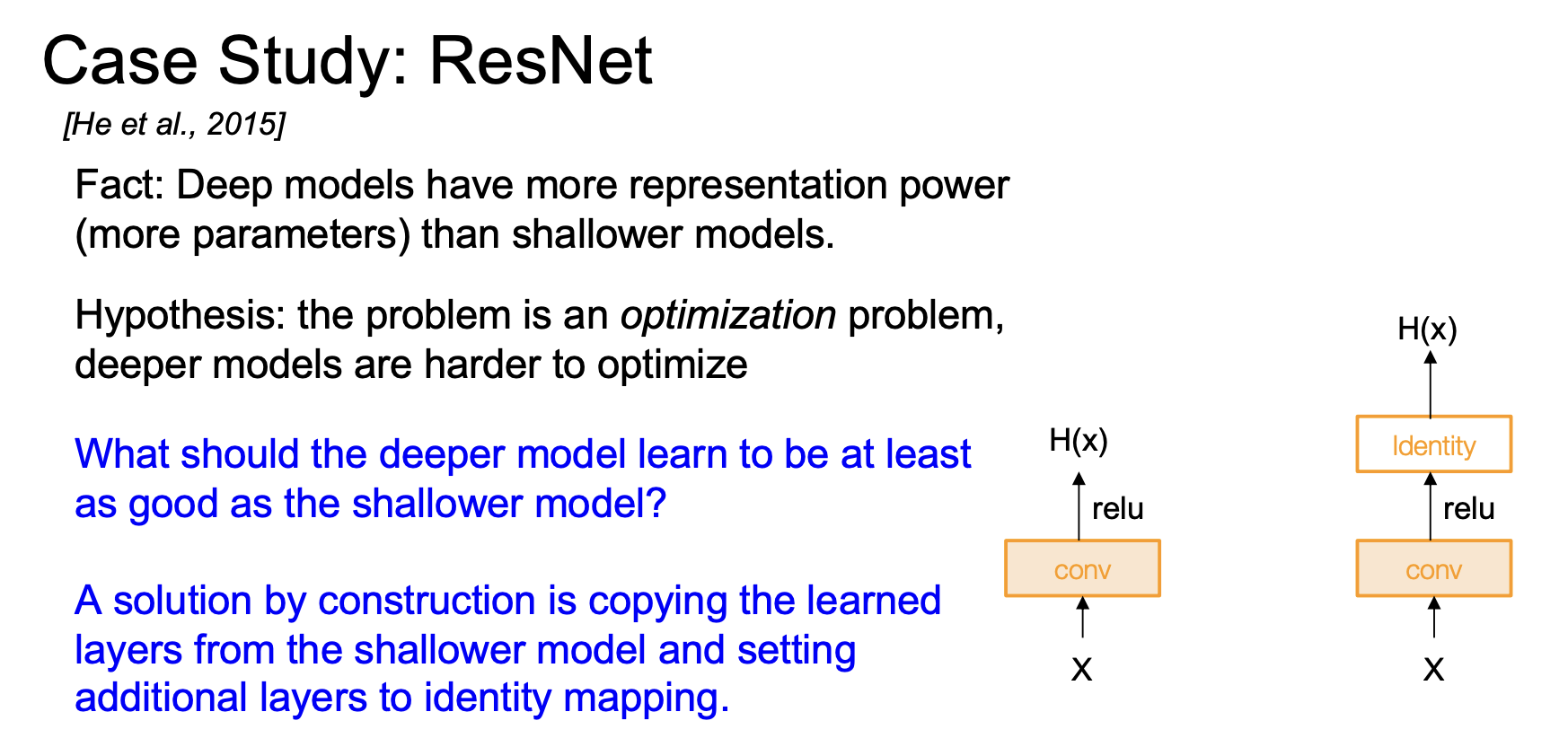
那么我们如何将这种直觉融入模型,我们希望它可以和浅层模型一样优秀,我们通过拟合来实现,所谓的残差映射,而非直接拟合底层映射
直觉是一种观察到的现象,这些大型网络在训练和测试误差上表现更差,因为它们难以优化,因此直觉是我们需要构建能够轻松模拟浅层网络的模型,使其至少与浅层模型一样好,它们通过添加残差连接实现了这一点,以便轻松复制值,将其融入架构本身,而不是在卷积层之间学习恒等映射
如何初始化各层的权重值
Kaiming初始化
1
2
3
4
5
6
7
| dims = [4096] * 7
hs = []
x = np.random.randn(16,dims[0])
for Din,Dout in zip(dims[:-1], dims[1:]):
W = np.random.randn(Din,Dout) * np.sqrt(2/Din)
x = np.maximum(0,x,dot(W))
hs.append(x)
|
图像归一化要点总结:对每个通道进行居中和缩放
- 对每个通道减去均值
- 再除以每个通道的标准差(每个通道各自统计,共 三个数)
- 需要预先计算:针对你的数据集,为每个像素通道计算均值和标准差
norm_pixel[i,j,c] = (pixsl[i,j,c] - np.mean(pixel[:,:,c])) / np.std(pixel[:,:,c])
正则化
训练:加入某种形式的随机性
$$
y = f_w(x, z)
$$测试:对随机性取平均
$$
y = f(x) = E_z [ f(x, z) ] = \int p(z) f(x, z) dz
$$数据增强
1.水平翻转
这对日常物体很有用,因为大多数物体具有对称性
2.调整大小和缩减,方案如下











