反向传播
反向传播是计算梯度的一种方法,这种方法需要利用计算图,计算图的每个节点表示我们执行的每一步计算,例如上一讲讲的损失函数的计算图如下
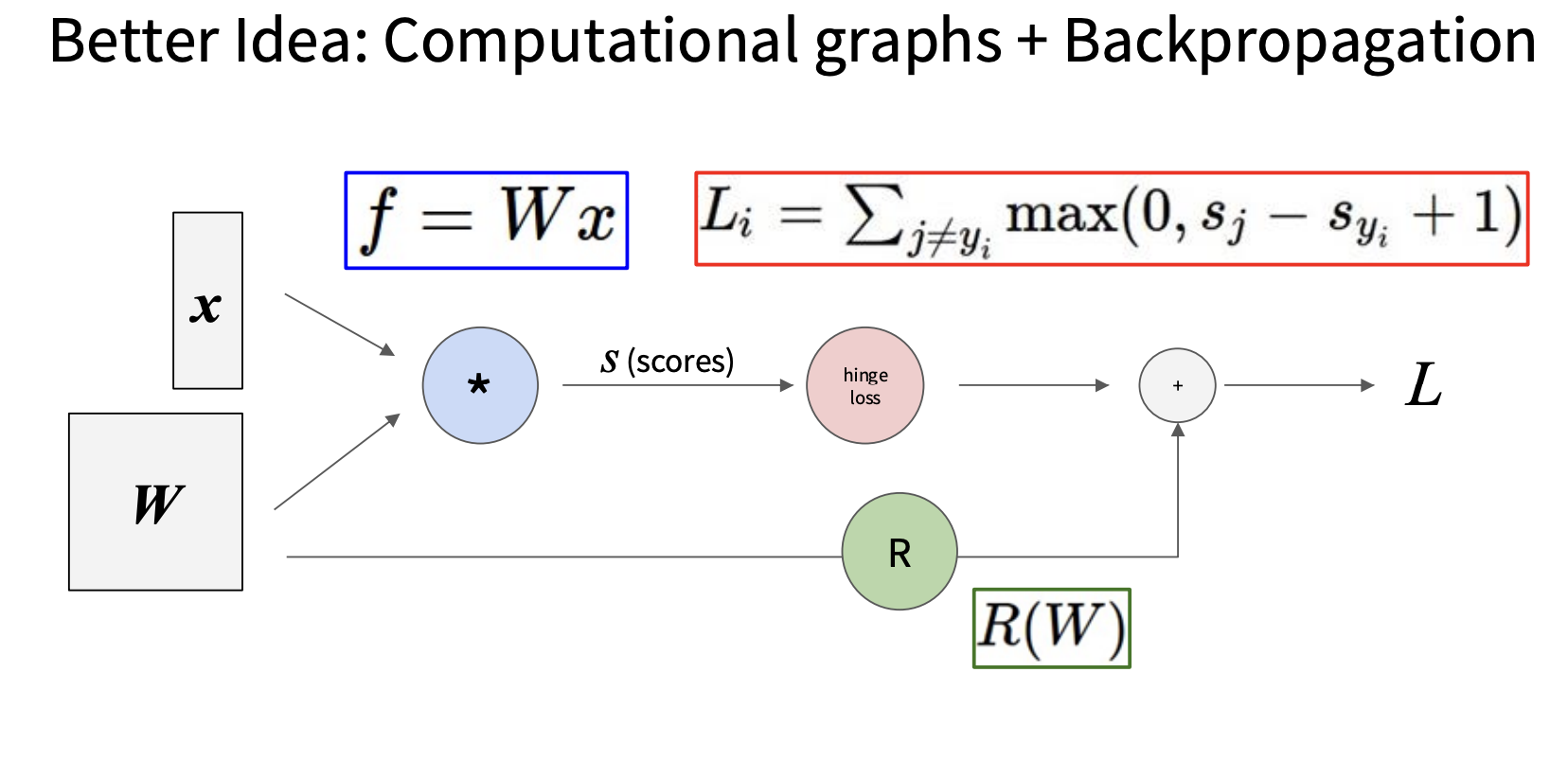
第一个节点计算得分s,第二个节点计算折页损失,最后一个节点计算总损失(加上正则项)
计算图的计算步骤分为前向传播以及反向传播,刚刚描述的步骤为前向传播,现在我们结合下图理解反向传播计算梯度的思路
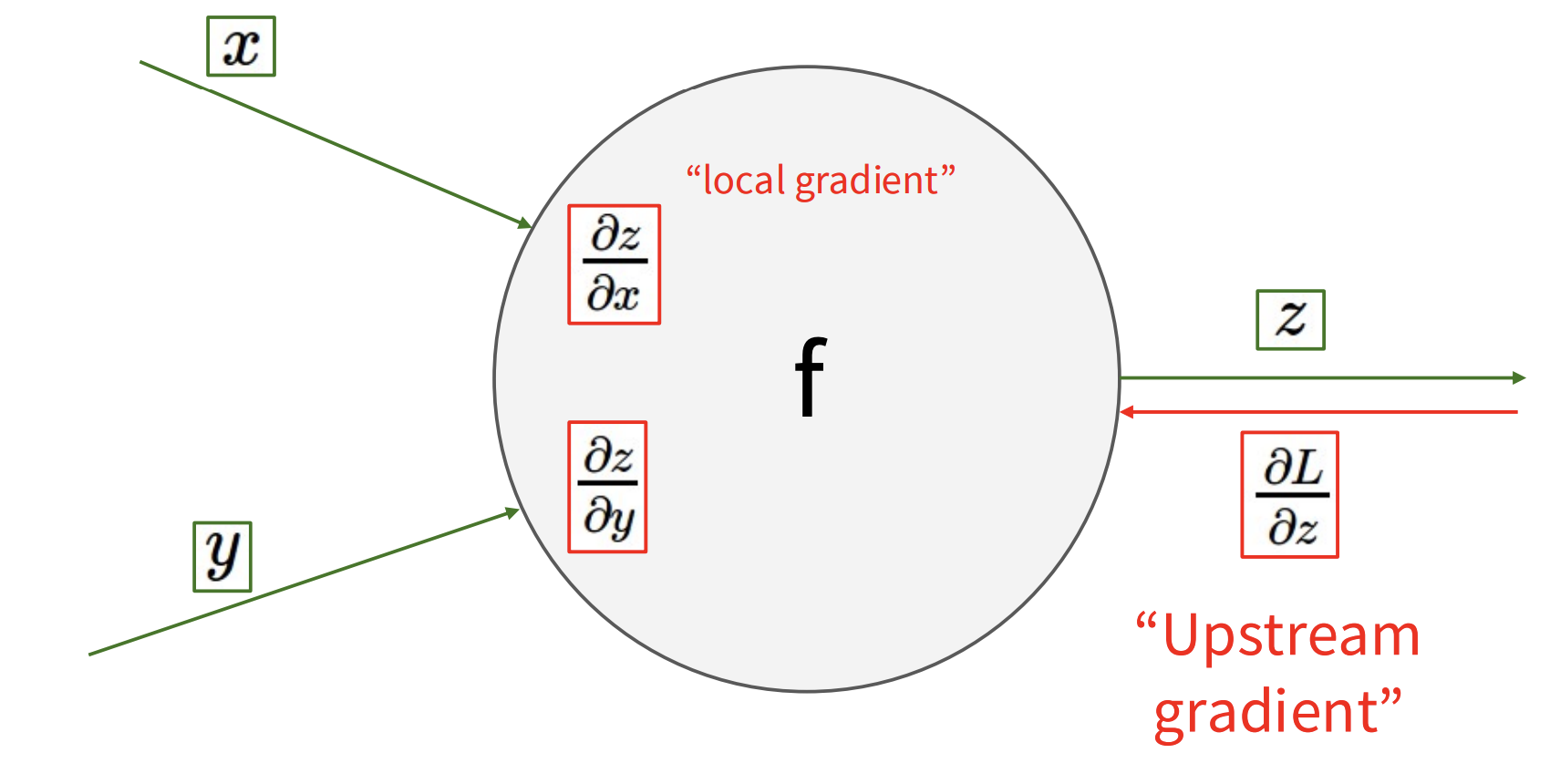
对于每个节点,假设我们已知输出的梯度$\frac{\partial L}{\partial z}$,现在我们要计算输入的梯度$\frac{\partial L}{\partial x}$,$\frac{\partial L}{\partial y}$,计算的思路很简单,利用链式法则,首先计算“局部梯度”$\frac{\partial z}{\partial x}$,$\frac{\partial z}{\partial y}$,然后利用链式法则可得
$$ \frac{\partial L}{\partial x} =\frac{\partial L}{\partial z}\,\frac{\partial z}{\partial x}\,\frac{\partial L}{\partial y} =\frac{\partial L}{\partial z}\,\frac{\partial z}{\partial y} $$计算过程如下图所示
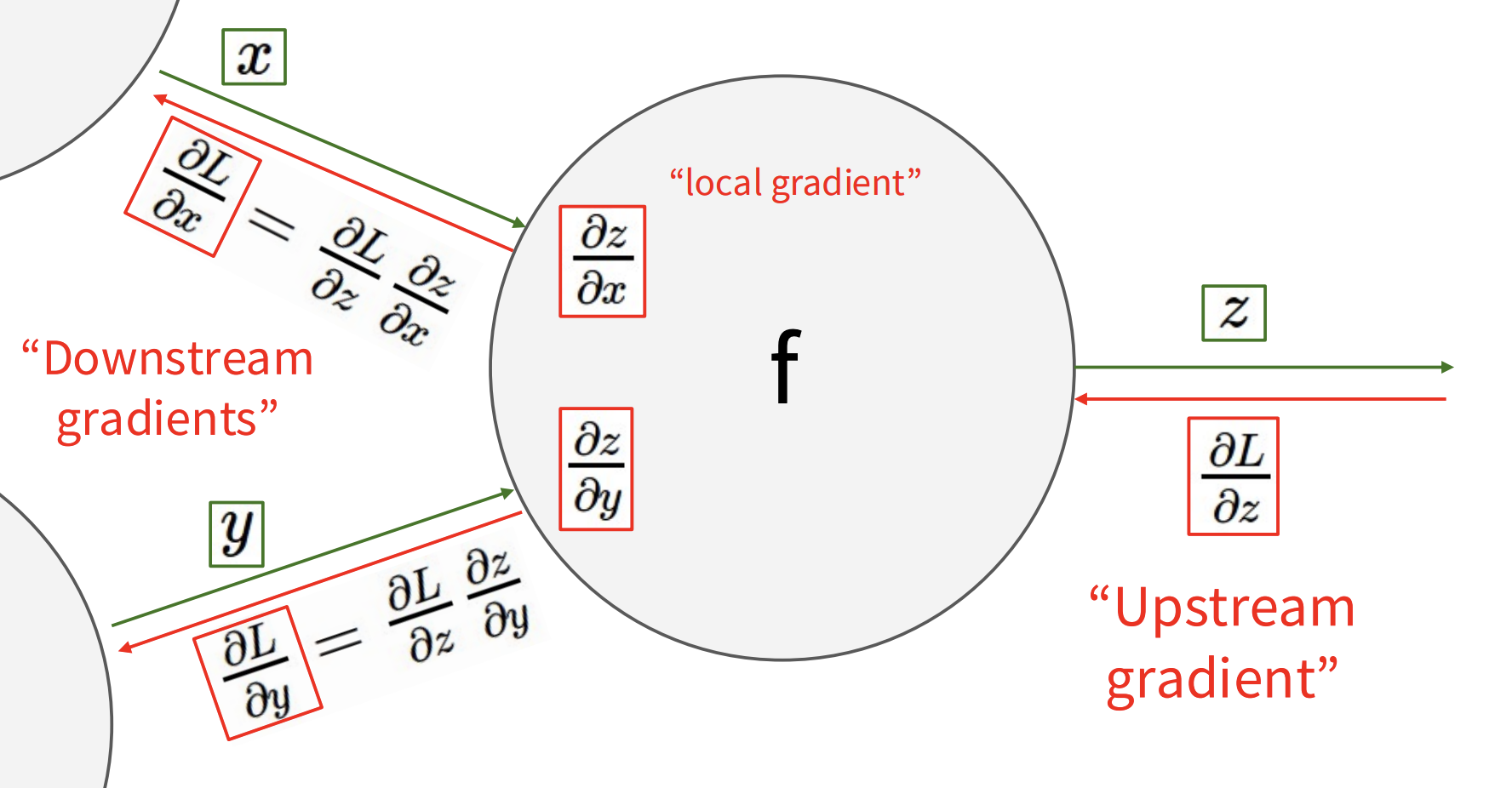
如果节点有多个输出$z_j$,那么输入的梯度$\frac{\partial L}{\partial x}$,$\frac{\partial L}{\partial y}$需要累加,具体公式为
$$ \frac{\partial L}{\partial x} = \sum_{j} \frac{\partial L}{\partial z_{j}} \,\frac{\partial z_{j}}{\partial x}, \qquad \frac{\partial L}{\partial y} = \sum_{j} \frac{\partial L}{\partial z_{j}} \,\frac{\partial z_{j}}{\partial y} $$计算过程如下图所示
