Bits
为什么要用比特
- 易于用双稳态元件存储
- 能在有噪声且不精确的电线上可靠传输
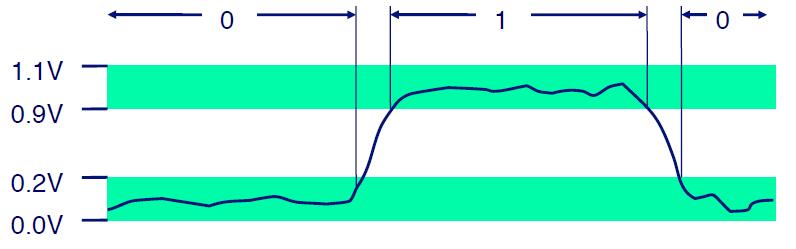
我们可以用二进制来表示浮点数。在一个二进制的小数中:
- 小数点左边的第一位权重为 2^0,向左依次为 2^1、2^2、…
- 小数点右边的第一位权重为 2^-1,向右依次为 2^-2、2^-3、…
因此,如果将数字写成 32 位或者 64 位的字符串会很麻烦。通常将 4 bits 为一组,用十六进制表示。这样十六进制与二进制的转换就非常方便。

字节
- 一个字节等于 8 比特
布尔代数
- 比特之间的关系(操作)
- 1 代表 true,0 代表 false

Example:表示与操作集合
- 表示方式:
- 一个长度为 $w $的位向量表示集合 ${0, 1, …, w-1}$ 的子集
- 如果 $a_j = 1,j ∈ A$
- for example:{0, 3, 5, 6}
- 01101001
- 76543210
对于上面的这个例子,“01101001”代表的就是 “76543210” 中各个位的数字在集合中是否出现,出现即为 1,反之为 0。
对比逻辑运算符
- &&、||、 !
Example:
- !0x41 → 0x00
- !0x99 → 0x01
- !!ox41 → 0x01
- 0x69 && 0x55 → 0x01
- p && *p(避免空指针访问,如果 p 是 NULL,就不会解引用)
移位操作
左移:x « y
- 向左移动位次,多余的bits扔掉,添加相对应数目的0
右移:x » y
逻辑右移
- 和左移类似
算数右移
- 若第一个数为1,把原本填充的0改为填充1
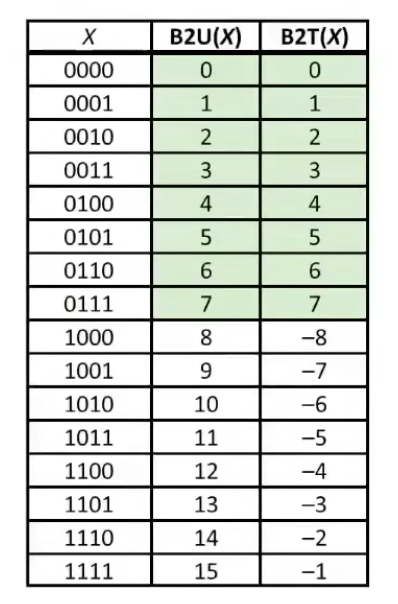
整数编码
无符号数
$B2U(X) = \sum_{i = 0}^{w-1} x_i \cdot 2^i $
补码(Two’s Complement)
$B2T(X) = -x_{w-1} \cdot 2^{w-1} + \sum_{i=0}^{w-2} x_i \cdot 2^i$
数值范围
W = 16
| Value Type | Formula / Binary Pattern | Decimal | Hex | Binary |
|---|---|---|---|---|
| Unsigned Values | ||||
| UMin | 0 | 0 | 0x0000 | 00000000 00000000 |
| UMax | 2W - 1 | 65535 | 0xFFFF | 11111111 11111111 |
| Two’s Complement Values | ||||
| TMin | -2W-1 / 100…0 | -32768 | 0x8000 | 10000000 00000000 |
| TMax | 2W-1 - 1 / 011…1 | 32767 | 0x7FFF | 01111111 11111111 |
| Other Values | ||||
| -1 | 111…1 | -1 | 0xFFFF | 11111111 11111111 |
| 0 | 000…0 | 0 | 0x0000 | 00000000 00000000 |
因此我们可以得到一个关系如下:
$TMin = TMax + 1$
$UMax = 2 \times TMax + 1$
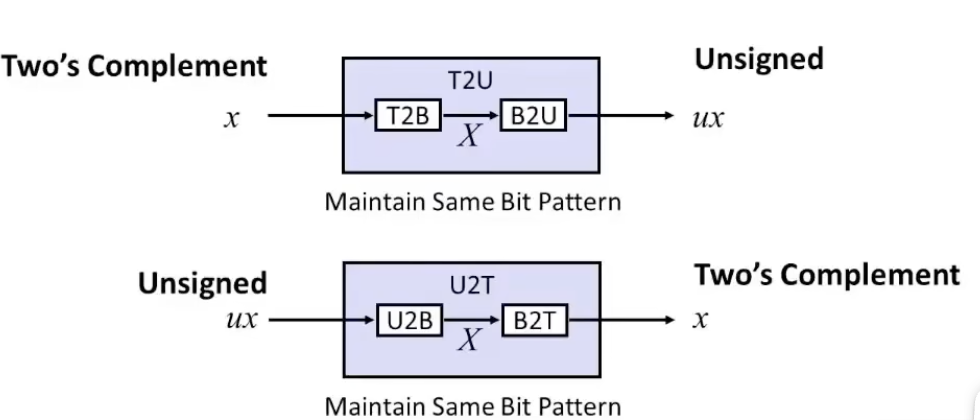
转换
有符号整型和无符号整型和十进制的转换关系如下:
显然上述转换是可逆的:
- $\text{U2B}(x)=\text{B2U}^{-1}(x)$
- $\text{T2B}(x)=\text{B2T}^{-1}(x)$
利用复合关系可以得到有符号整型以及无符号整型的转换关系:
对于$\text {TMin} \leqslant x \leqslant \text{TMax}$
$$ T 2 U_w(x)=\left\{\begin{array}{ll} x+2^{w}, & x<0 \\ x, & x \geqslant 0 \end{array}\right. $$对于$0 \leqslant x \leqslant \text{UMax}$
$$ U 2 T_{w}(u)=\left\{\begin{array}{ll} u, & u \leqslant \text{TMax} \\ u-2^{w}, & u>\text{TMax} \end{array}\right. $$下图为补码到无符号数的转换关系
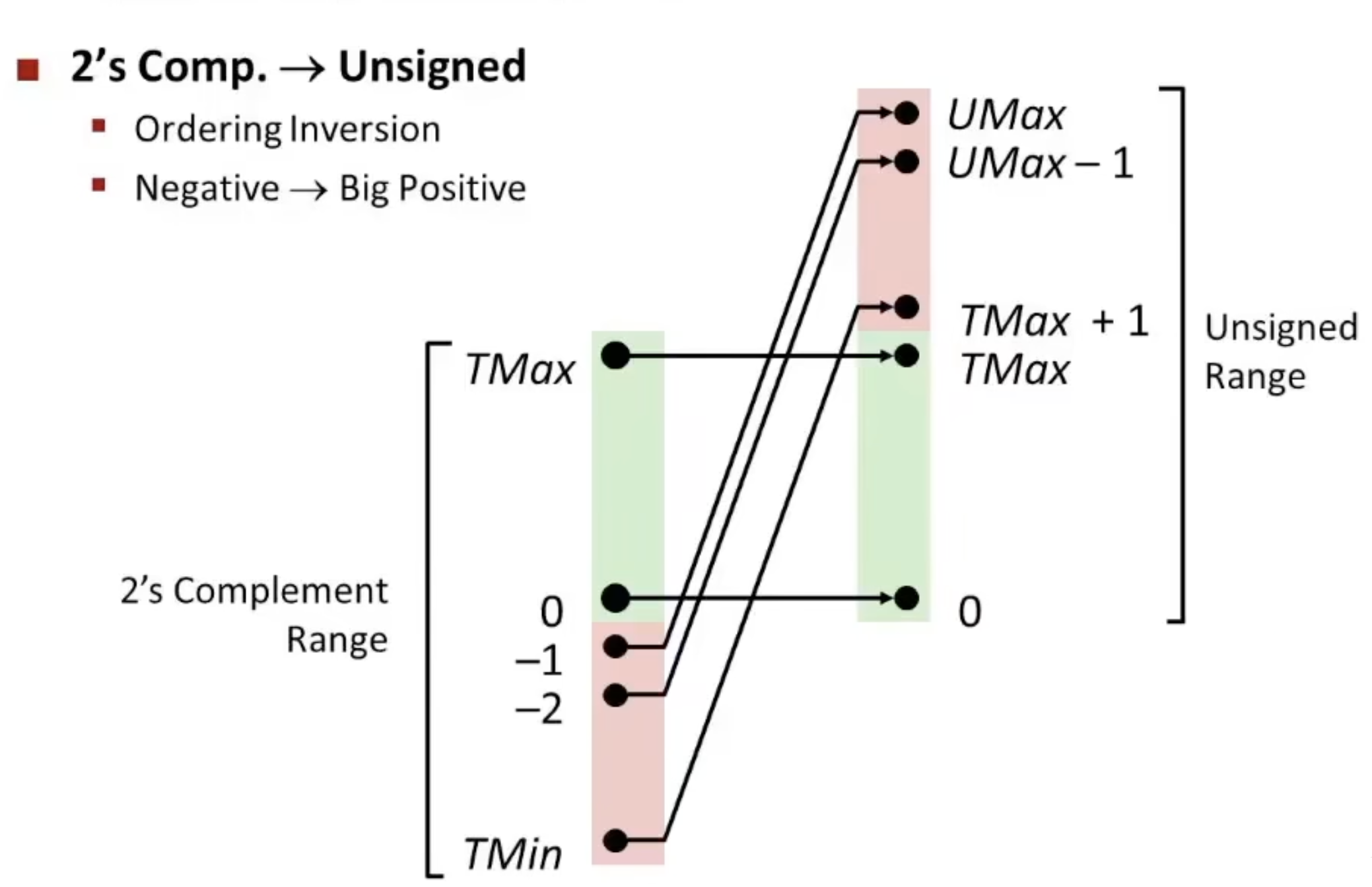
C语言中的转换如下:
| |
表达式求值规则
若单个表达式中同时出现无符号数与有符号数,则有符号值会被隐式转换为无符号数(包括比较运算
<、>、==、<=、>=)。
举例:W = 32 位
常量定义
TMIN = -2,147,483,648TMAX = 2,147,483,647
| 常量 1 | 常量 2 | 实际类型 | 关系 | 结果 | 说明 |
|---|---|---|---|---|---|
0 | 0U | 无符号 | < | 假 | 两者均为 0 |
-1 | 0 | 有符号 | < | 真 | 普通有符号比较 |
-1 | 0U | 无符号 | > | 真 | -1 被转成 4294967295U |
2147483647 | -2147483648 | 有符号 | > | 真 | 普通有符号比较 |
2147483647U | -2147483648 | 无符号 | < | 真 | -2147483648 被转成 2147483648U |
-1 | -2 | 有符号 | > | 真 | 普通有符号比较 |
(unsigned)-1 | -2 | 无符号 | > | 真 | -2 被转成 4294967294U |
2147483647 | 2147483648U | 无符号 | < | 真 | 前者 < 后者 |
2147483647 | (int)2147483648U | 有符号 | > | 真 | 后者溢出成 -2147483648 |
小结:有符号与无符号强制转换的基本规则
位模式保持不变
强制转换时,内存中的 0/1 序列原样复制。仅重新解释
同一段位模式,按目标类型(有符号或无符号)重新解读。可能产生“意外”
数值可能突然加上或减去 2^W(W 为位数)。表达式中的混合类型
只要表达式里同时出现signed int与unsigned int,编译器会把signed int隐式转换成unsigned int,再参与运算。
扩展,截断
扩展
无符号扩展至需要在前面的bits补0,有符号扩展如下
任务:
- 给定w-bit的有符号整型x
- 将其转换为w+k-bit的有符号整型,值不变
规则:
将符号位复制k份
$X’ = X_{w-1},\dots,X_{w-1},X_{w-1},X_{w-2},\dots,X_0$
补码的符号扩展
定义宽度为 $w$ 的位向量 $\vec{x} = [x_{w-1}, x_{w-2}, \dots, x_0]$ 和宽度为 $w’$ 的位向量 $\vec{x}’ = [x’{w’-1}, x’{w’-2}, \dots, x’0]$,其中 $w’ > w$。则$B2T_w(\vec{x}) = B2T{w’}(\vec{x}’)$,
补码数值的符号扩展
令$w’ = w + k$,我们想要证明的是
$$ B2T_{w+k} ([x_{w-1}, \cdots, x_{w-1}, x_{w-2}, \cdots, x_0]) = B2T_w([x_{w-1}, x_{w-2}, \cdots, x_0]) $$下面的证明是对$k$进行归纳。也就是说,如果我们能够证明符号扩展一位保持了数值不变,那么符号扩展任意位都能保持这种属性。因此,证明的任务就变为了:
$$ B2T_{w+1} ([x_{w-1}, x_{w-1}, x_{w-2}, \cdots, x_0]) = B2T_w([x_{w-1}, x_{w-2}, \cdots, x_0]) $$展开左边的表达式,得到:
$$ \begin{aligned} B2T_{w+1} ([x_{w-1}, x_{w-1}, x_{w-2}, \cdots, x_0]) &= -x_{w-1}2^w + \sum_{i=0}^{w-1}x_i2^i \\ &= -x_{w-1}2^w + x_{w-1}2^{w-1} + \sum_{i=0}^{w-2}x_i2^i \\ &= -x_{w-1}(2^w - 2^{w-1}) + \sum_{i=0}^{w-2}x_i2^i \\ &= -x_{w-1}2^{w-1} + \sum_{i=0}^{w-2}x_i2^i \\ &= B2T_w([x_{w-1}, x_{w-2}, \cdots, x_0]) \end{aligned} $$我们使用的关键属性是$2^w - 2^{w-1} = 2^{w-1}$。因此,加上一个权值为$-2^w$的位,和将一个权值为 $-2^{w-1}$的位转换为一个权值为 $2^{w-1}$ 的位,这两项运算的综合效果就会保持原始的数值。
截断
无符号截断
原始 $w$ 位:
截断为 $k$ 位后:
推导
$$ \begin{aligned} B2U_w([x_{w-1}, x_{w-2}, \cdots, x_0]) \mod 2^k &= \left[ \sum_{i=0}^{w-1} x_i 2^i \right] \mod 2^k \\ &= \left[ \sum_{i=0}^{k-1} x_i 2^i \right] \mod 2^k \\ &= \sum_{i=0}^{k-1} x_i 2^i \\ &= B2U_k([x_{k-1}, x_{k-2}, \cdots, x_0]) \end{aligned} $$有符号截断
原始 $w$ 位:
截断为 $k$ 位后:
