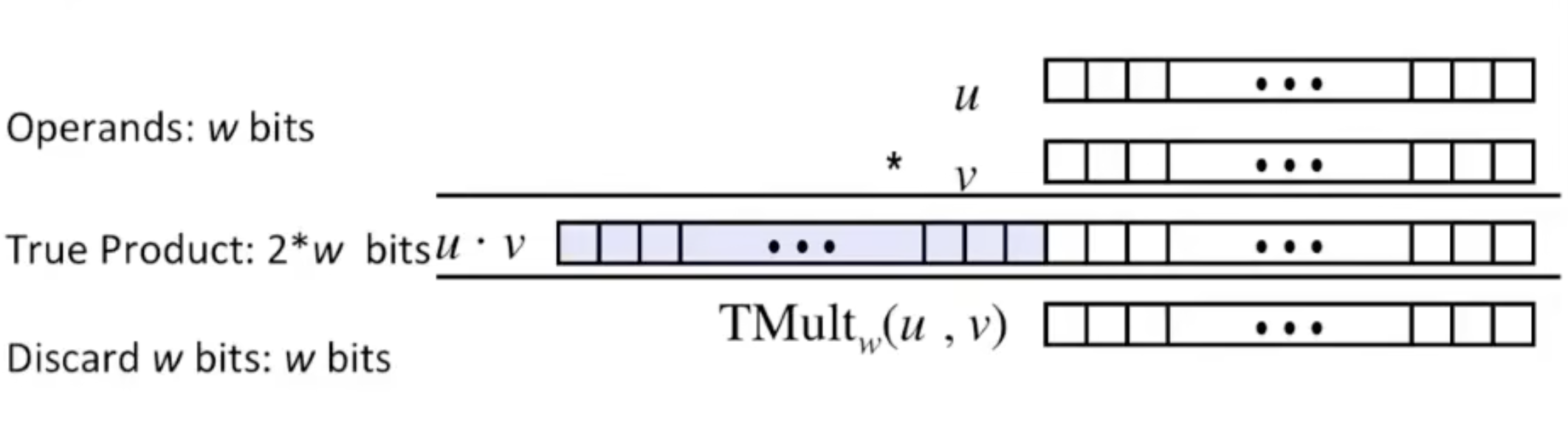
加法
无符号加法
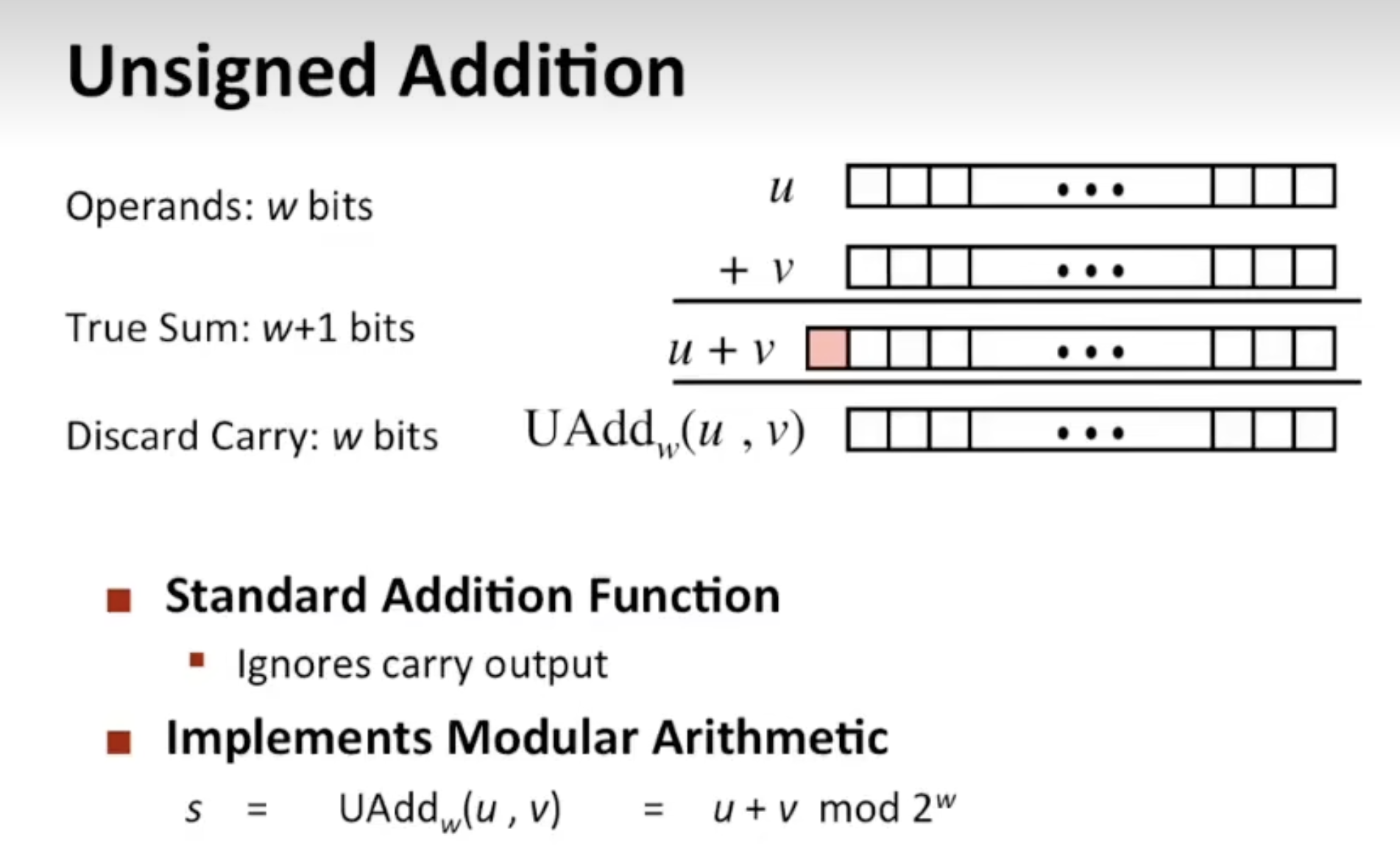
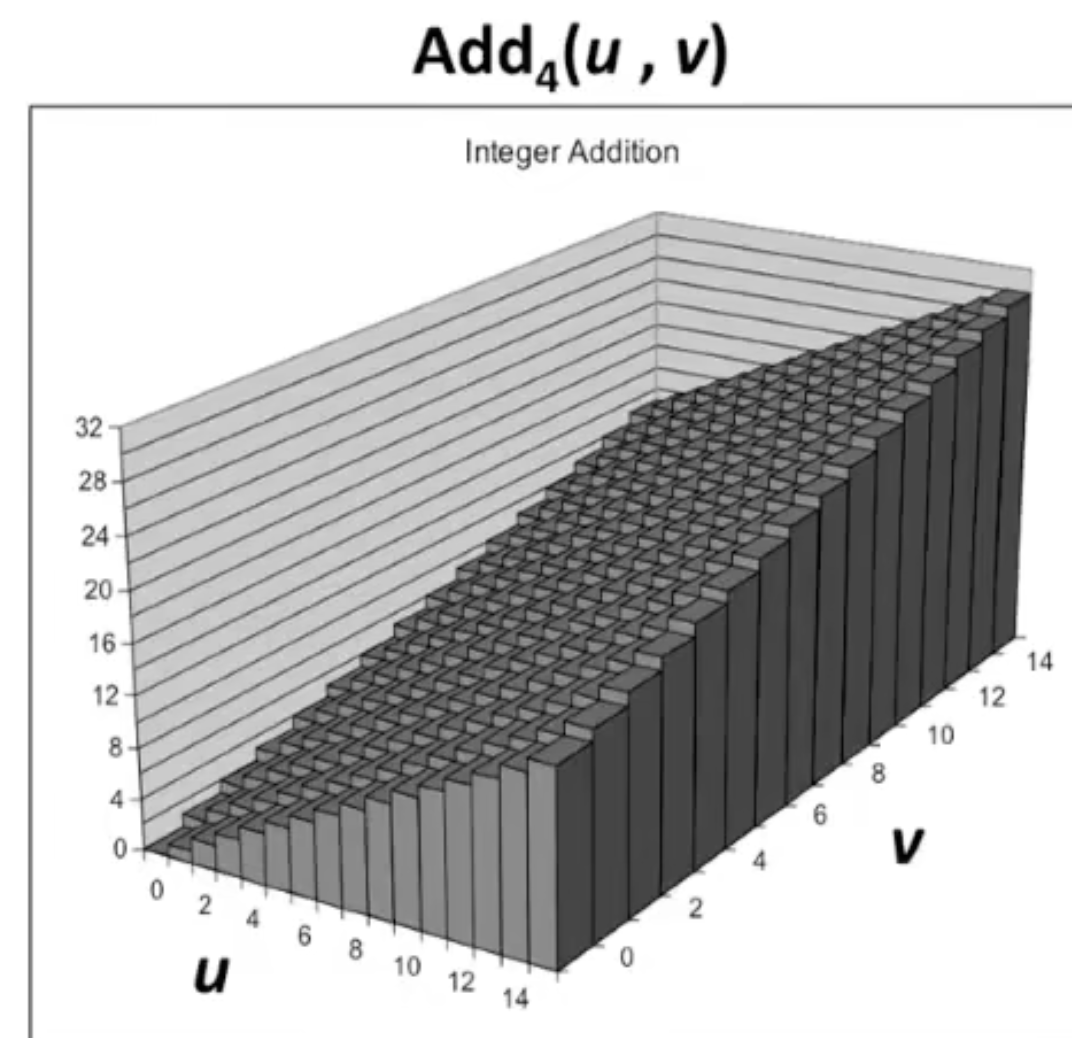
无符号的加法很简单,和二进制加法一样,只不过要把overflow的删除,并且把结果取模即可
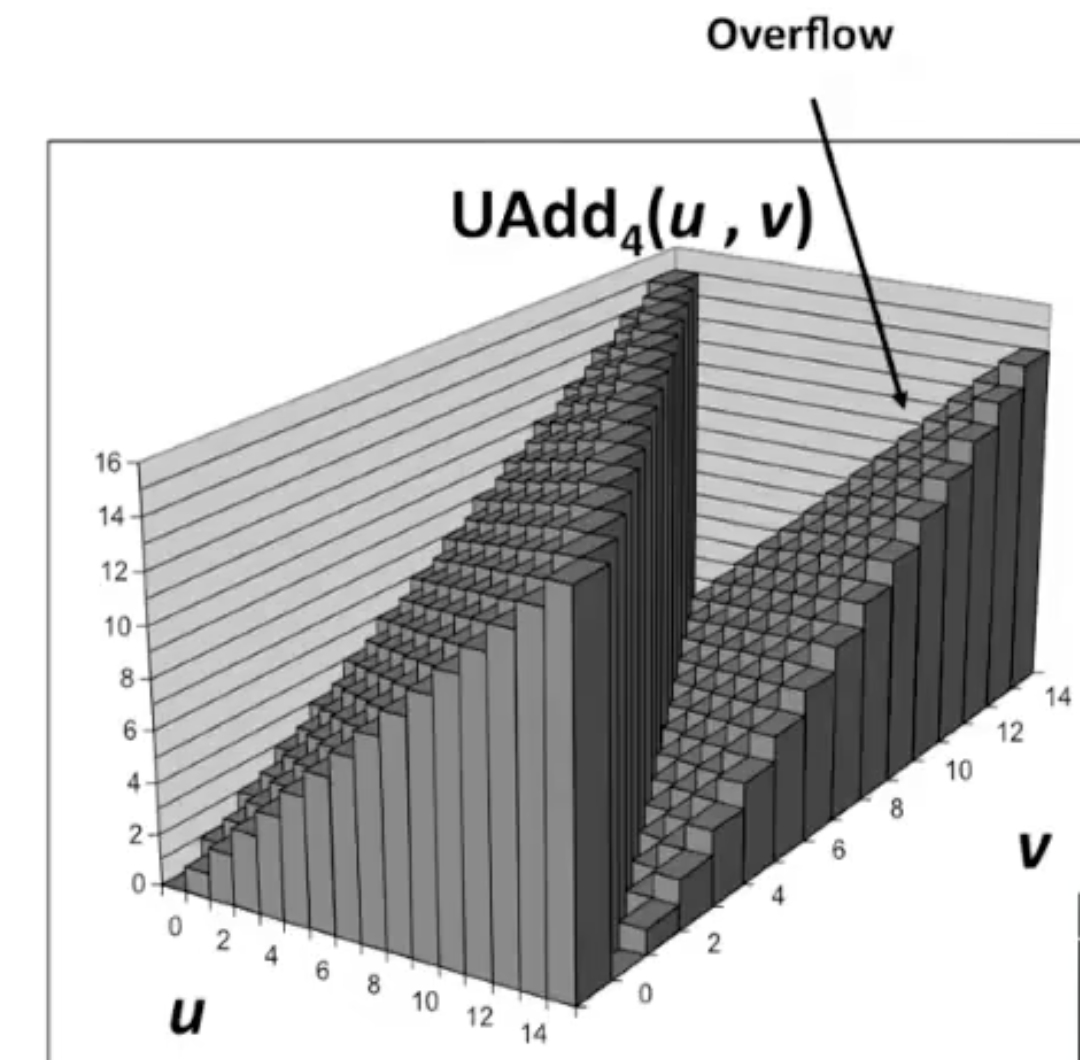
检测无符号数中加法的溢出
令 $s = U +_w^u V$ 为无符号整数 $U$ 和 $V$ 的和,那么当且仅当 $s < U$(或等价的 $s < V$)时产生溢出,这是因为:
$$ \begin{aligned} s &= U + V - 2^w < U \\ s &= U + V - 2^w < V \end{aligned} $$补码加法

对满足 $-2^{w-1} \leq x$,$y \leq 2^{w-1}-1$ 的整数 $x$ 和 $y$,有:
$$ x +_w^t y = \begin{cases} x + y - 2^w, & 2^{w-1} \leq x + y \quad \text{正溢出} \\ x + y, & -2^{w-1} \leq x + y < 2^{w-1} \quad \text{正常} \\ x + y + 2^w, & x + y < -2^{w-1} \quad \text{负溢出} \end{cases} $$两个数的$w$位补码之和与无符号之和有完全相同的位级表示
利用左移做乘法
- 大多数机器中左移比乘法快
- 编译器会自动生成这样的代码
方法的证明:
假设 $x$ 的 $w$ 位二进制表示为 $\left[x_{w-1}, x_{w-2}, \cdots, x_{0}\right]$,那么 $\left[x_{w-1}, x_{w-2}, \cdots, x_{0}, 0, \cdots, 0\right]$ 给出了 $x2^k$ 的 $w+k$ 位二进制表示:
$$ \begin{aligned} B2U_{w+k}\left(\left[x_{w-1}, x_{w-2}, \cdots, x_{0}, 0, \cdots, 0\right]\right) &= \sum_{i=0}^{w-1} x_{i} 2^{i+k} \\ &= \left[\sum_{i=0}^{w-1} x_{i} 2^{i}\right] \cdot 2^{k} \\ &= x 2^{k} \end{aligned} $$对于固定长度的表示,高 $k$ 位被丢弃,左移 $k$ 位的二进制表示为
$$ \left[x_{w-k-1}, x_{w-k-2}, \cdots, x_{0}, 0, \cdots, 0\right] $$所以
$$ \begin{aligned} B2U_{w}\left(\left[x_{w-k-1}, x_{w-k-2}, \cdots, x_{0}, 0, \cdots, 0\right]\right) &= \sum_{i=0}^{w-k-1} x_{i} 2^{i+k} \\ &= \left[\sum_{i=0}^{w-k-1} x_{i} 2^{i}\right] \cdot 2^{k} \\ &= \left[\sum_{i=0}^{w-1} x_{i} 2^{i}\right] \cdot 2^{k} \mod 2^w \\ &= x2^k \mod 2^w \end{aligned} $$所以对于无符号整数
$$ B2U_{w}\left(\left[x_{w-k-1}, x_{w-k-2}, \cdots, x_{0}, 0, \cdots, 0\right]\right) = \text{UMult}_w(x,2^k) $$对于有符号整数,利用
$$ \text{TMult}_w(u,v) = U2T_w((u \cdot v) \mod 2^w) $$可以得到相同的结果。
一般情形
现在考虑一般的情形,假设我们需要计算 $u \times K$,其中 $K$ 为常数,将 $K$ 表达为一组 $0$ 和 $1$ 交替的序列
$$ [(0 \cdots 0)(1 \cdots 1)(0 \cdots 0) \cdots (1 \cdots 1)] $$考虑一组从位置 $n$ 到位置 $m$ 的连续 $1$,那么可以用如下方式计算这部分的对于乘积的影响:
$$ \begin{aligned} &(x << n) + (x << (n-1)) + \cdots + (x << m) \\ &(x << (n+1)) - (x << m) \end{aligned} $$移位操作和二进制乘除法的联系
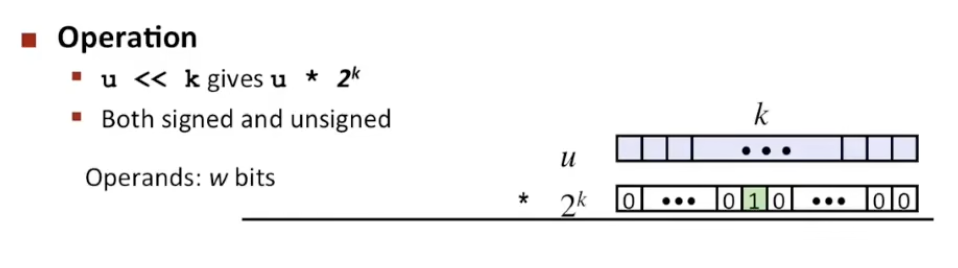
使用移位操作代替除以 2 的幂(无符号)
- $u » k$ 给出 $\lfloor u / 2^{k} \rfloor$
- 使用逻辑移位
证明:
假设 $x$ 的 $w$ 位二进制表示为 $\left[x_{w-1}, x_{w-2}, \cdots, x_{0}\right]$,右移 $k$ 位的二进制表示为 $\left[0, \cdots, 0, x_{w-1}, x_{w-2}, \cdots, x_{k}\right]$
$$ \begin{aligned} B2U_w(\left[0, \cdots, 0, x_{w-1}, x_{w-2}, \cdots, x_{k}\right]) &= \sum_{i=0}^{w-k-1} x_{i+k} 2^{i} \\ B2U_{w}\left(\left[x_{w-1}, x_{w-2}, \cdots, x_{0}\right]\right) &= \sum_{i=0}^{w-1} x_{i} 2^{i} \\ &= 2^k \sum_{i=0}^{w-k-1} x_{i+k} 2^{i} + \sum_{i=0}^{k-1} x_{i} 2^{i} \\ &= 2^k B2U_w(\left[0, \cdots, 0, x_{w-1}, x_{w-2}, \cdots, x_{k}\right]) + \sum_{i=0}^{k-1} x_{i} 2^{i} \end{aligned} $$所以
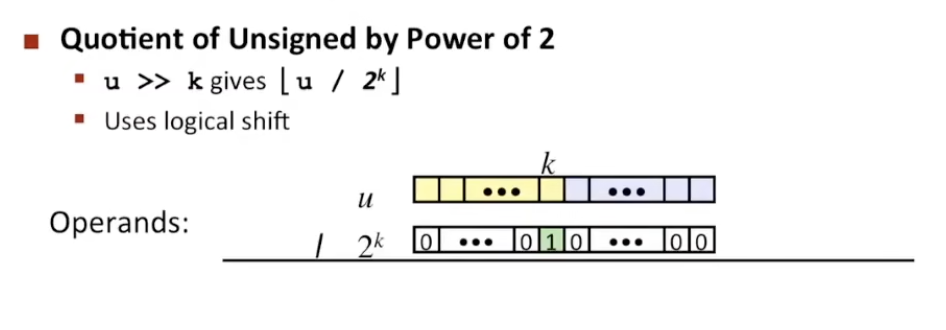
$$ \lfloor x / 2^{k} \rfloor = x >> k $$使用移位操作代替除以 2 的幂(有符号)
- $u » k$ 给出 $\lfloor u / 2^{k} \rfloor$
- 使用算数移位
当 $u > 0$ 时上述方法和无符号情形一致,但是当 $u < 0$ 时则会产生有问题的结果,例如取 $u = -12340$:
考虑 $k=4,8$ 时的结果,在 C 语言中实际结果为 $-771$ 和 $-48$,之所以和 C 语言中的结果不同,是因为上述算法朝着离 $0$ 更远的方向舍入,所以当 $u < 0$ 时要向上舍入,达到上述效果利用如下事实即可
$$ \lceil x / y \rceil = \lfloor (x + y - 1) / y \rfloor $$Unsigned
必须做一个明确的分配而不是暗示
容易犯错误,例如下面的代码会出现无限循环
1 2 3unsigend i; for(i = cnt - 2;i >= 2;i --) a[i] += a[i + 1];可能会变的很诡异
1 2 3#define DELTA sizeof(int)//默认int的size是一个unsigned的size_t int i; for(i = CNT;i - DELTA >= 0;i -=DELTA)//和上面的代码出现一样的问题
正确的代码如下
| |
什么时候用无符号整数
执行模块化算术时使用
- 多精度算术
在使用位表示集时使用
- 逻辑右移,无符号扩展
(最好不要用unsigned)
内存中数字的一些底层表示
Word Size
硬件本身并不一定定义字长大小
任何给定的计算机都具有字长
直到现在,大部份机器都采用32 bits(4 bytes)作为字长
- 地址限制为4 GB($2^{32}$bytes)
越来越多机器具有64位字长
机器仍然支持多种数据格式
- 字长的分数或整数倍
- 但总是整数比特

比特顺序
分为大端法和小端法
- Example
- 变量x的value是0x01234567
- 地址是0x100